Regressão múltipla

A regressão simples pertence a uma variável dependente (y) e a uma variável independente (x). Regressão múltipla (também conhecido como regressão multivariáveis) pertence a uma variável dependente (resultado) e algumas variáveis independentes (também chamadas variáveis explicativas, preditores, regressores ou covariáveis). A regressão multivariada pertence a múltiplas variáveis dependentes e múltiplas variáveis independentes (veja mais no link).

Assim, regressão múltipla é uma coleção de técnicas estatísticas para construir modelos que descrevem de maneira razoável relações entre duas ou mais variáveis explicativas de um determinado processo. Admite-se que “Y” é a variável resposta (dependente) e “X1”, “X2”, etc, são as variáveis preditoras (independentes), onde os valores esperados de Y são dados por uma combinação linear das variáveis preditoras. Uma relação não-linear (como uma relação polinomial, por exemplo), mesmo envolvendo apenas uma variável preditora e a variável resposta, pode ser facilmente tratada no âmbito de uma regressão linear múltipla.

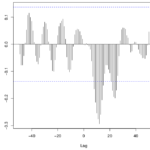
Quando existe uma relação entre as séries, nem sempre ocorre no mesmo ponto do tempo: muitas vezes um fenômeno antecede outro. Por isso, a correlação entre as séries não deve ser feita apenas pelo coeficiente de correlação usual (Pearson), devendo ser utilizada a função de correlação cruzada (CCF, cross-correlation function). A CCF parte do mesmo raciocínio da ACF (autocorrelation function, ou função de autocorrelação), mas com a diferença de que agora o objetivo é estudar a correlação entre uma série X(t) e uma outra série deslocada no tempo Y(t+1), Y(t+2). Uma análise do gráfico de correlação cruzada permite estimar a necessidade e o valor da defasagem (ou “lag”) entre cada variável independente e a dependente. Veja mais no post sobre Correlação.

ARIMAX

Pode-se usar um modelo ARIMA como um modelo de regressão que inclui uma correção para erros auto-correlacionados. Se seus gráficos ACF e PACF residuais exibem uma “assinatura” autoregressiva ou de média móvel identificável (por exemplo, algum padrão significativo de autocorrelações e/ou autocorrelações parciais nos primeiros intervalos e/ou desfasamento sazonal), então você pode considerar adicionar termos ARIMA (atrasos da variável dependente e/ou os erros) ao modelo de regressão para eliminar a autocorrelação e reduzir ainda mais o erro quadrático médio.

Para fazer isso, você simplesmente ajustaria o modelo de regressão como um modelo ARIMA com regressores, e você especificaria os termos AR e/ou MA apropriados para se adequarem ao padrão de autocorrelação que você observou nos resíduos originais. A maioria dos softwares de previsão oferece uma ou mais opções para combinar os recursos do ARIMA e modelos de regressão múltipla. Uma expansão dos modelos ARIMA que acrescenta um componente linear em função das observações das covariáveis é conhecido como ARIMAX.

Quando você adiciona um regressor a um modelo ARIMA, literalmente é adicionado apenas o regressor ao lado direito da equação de previsão ARIMA. Assim, a parte AR do modelo (e também a transformação de diferenciação, se houver) é aplicada à variável X exatamente da mesma maneira que é aplicada à variável Y antes que X seja multiplicado pelo coeficiente de regressão. Isso efetivamente significa que o modelo ARIMA é ajustado aos erros da regressão de Y em X (ou seja, a série “Y – beta*X”).

Veja esse exemplo para um modelo estacionário ARMA(1,1), onde o termo referente ao vetor da covariável X é acrescentado:

\(Y_t=\omega Z_t+\beta_0+\beta_1X_{t-1}-\alpha_1\epsilon_{t-1}+\epsilon_t\)

Onde α₁ é o coeficiente de médias móveis, β₀ e β₁ são os coeficientes autorregressivos e ε_t é erro aleatório associado (não correlacionado) no instante t. O coeficiente ω está associado a X no instante t, e sua magnitude não tem uma interpretação direta do efeito de X sobre Y. Usa-se a mesma ideia para obter o modelo ARIMAX (adicionando preditores) e/ou SARIMAX (adicionando sazonalidade) e para adição de uma matriz de covariáveis.

Projeção

Nos modelos ARIMA, as previsões são feitas a partir da equação do modelo obtido para os próximos h tempos (dias, meses, anos, etc). Para isto, é necessário obter a esperança condicional (soma do produto de cada probabilidade de saída da experiência pelo seu respectivo valor) de Y(t+h) dado X(t), X(t-1), etc. No modelo SARIMAX, são necessários os valores das covariáveis para obter as previsões.

Geralmente, a variância do erro da previsão aumenta ao longo do período predito, indicando que as previsões de curto prazo são mais precisas que as previsões de longo prazo. Veja algumas Métricas para comparar previsões clicando no link.

Fontes