Um processo é estacionário se todas as características do comportamento do processo não são alterados no tempo, ou seja, o processo se desenvolve aleatoriamente no tempo em torno da média, de modo que a escolha de uma origem dos tempos não é importante (suas propriedades não dependem do momento em que foi observada). A série estacionária (ou convergente) é o oposto da série não estacionária (ou divergente), onde ocorrem tendências ascendentes e descendentes e portanto a média e a variância são funções do tempo.
A classe dos modelos ARIMA é capaz de descrever de maneira satisfatória séries estacionárias e séries não estacionárias, desde que não apresentem um comportamento explosivo. Os processos estacionários homogêneos possuem o nível e/ou inclinação mudando com o decorrer do tempo ou também flutuando ao redor de um nível em um certo período, mas depois muda de nível e flutua ao redor de outro nível, e assim por diante.
Testes
Para verificar se uma série é estacionária, realiza-se um estudo da existência de alguma raiz dos operadores de retardos (utilizados em modelos de médias móveis) dentro do círculo unitário (denominada raiz unitária ou unit root). Um processo não-estacionário tem uma raiz unitária se 1 é raiz da equação característica do processo. Se as outras raízes da equação característica ocorrem dentro do círculo unitário – ou seja, têm um módulo (valor absoluto) menor que um –, então a primeira diferença do processo é estacionária.
Existem testes de raiz unitária que baseiam-se no seguinte teste de hipóteses:
- H0 (hipotese nula): Existe pelo menos uma raiz dentro do círculo unitário
- H1: Não existem raízes dentro do círculo unitário
No R, o pacote URCA possui as funções ur.df() e ur.kpss() que realizam os testes ADF e KPSS, respectivamente.
O teste de Dickey-Fuller Aumentado (ADF) testa a hipótese nula de se uma raiz unitária está presente em um modelo autorregressivo. A hipótese alternativa é diferente dependendo de qual versão do teste é usada: geralmente é estacionário, estacionário com intercepto (“drift”) ou estacionário com tendência (“trend”). Considerando que seja possível decompor a série em componentes de intercepto, tendência, número de defasagens e o coeficiente de presença de raiz unitária (delta), pode-se definir um estimador baseado em delta.
A função ur.df() realiza o cálculo dessa estatística. Ela recebe os parâmetros “type” (“none”, “drift” ou “trend”) e “selectlags”, que define a forma de seleção da defasagem (“Fixed”, “AIC” ou “BIC”) – no caso de “fixed”, deve-se usar o parâmetro “lags” com um número inteiro. A defasagem (ou lag) funciona da seguinte forma: para lag = 2, são calculadas as diferenças entre o terceiro e o primeiro valor, entre o quarto e o segundo valor, entre o quinto e o terceiro valor etc. Utilizando o comando dentro das funções print(summary()), são impressos na tela mais detalhes e o valor da estatística.
O resultado é um número negativo. Quanto mais negativo for, mais forte a rejeição da hipótese de que existe uma raiz unitária em algum nível de confiança – ou seja, mais distante de ser um processo estacionário.
Os valores críticos da estatística foram tabelados por Dickey e Fuller através de simulação Monte Carlo e variam nos casos de presença somente de intercepto (caso A), presença somente de tendência (caso B) e presença de ambos (caso C). Deve-se comparar o valor obtido com uma tabela com valores críticos conforme o caso, número de amostras (linhas) e as probabilidades de rejeição da hipótese nula (colunas) – fonte:
| n | 1% | 5% | 10% | 90% | 95% | 99% | |
|---|---|---|---|---|---|---|---|
| Caso A | 25 | -2.66 | -1.95 | -1.60 | 0.92 | 1.33 | 2.16 |
| (sem constante | 50 | -2.62 | -1.95 | -1.61 | 0.91 | 1.31 | 2.08 |
| sem tendência) | 100 | -2.60 | -1.95 | -1.61 | 0.90 | 1.29 | 2.03 |
| 250 | -2.58 | -1.95 | -1.61 | 0.89 | 1.29 | 2.01 | |
| 500 | -2.58 | -1.95 | -1.61 | 0.89 | 1.28 | 2.00 | |
| >500 | -2.58 | -1.95 | -1.61 | 0.89 | 1.28 | 2.00 | |
| Caso B | 25 | -3.75 | -3.00 | -2.62 | -0.37 | 0.00 | 0.72 |
| (constante | 50 | -3.58 | -2.93 | -2.60 | -0.40 | -0.03 | 0.66 |
| sem tendência) | 100 | -3.51 | -2.89 | -2.58 | -0.42 | -0.05 | 0.63 |
| 250 | -3.46 | -2.88 | -2.57 | -0.42 | -0.06 | 0.62 | |
| 500 | -3.44 | -2.87 | -2.57 | -0.43 | -0.07 | 0.61 | |
| >500 | -3.43 | -2.86 | -2.57 | -0.44 | -0.07 | 0.60 | |
| Caso C | 25 | -4.38 | -3.60 | -3.24 | -1.14 | -0.80 | -0.15 |
| (constante | 50 | -4.15 | -3.50 | -3.18 | -1.19 | -0.87 | -0.24 |
| tendência) | 100 | -4.04 | -3.45 | -3.15 | -1.22 | -0.90 | -0.28 |
| 250 | -3.99 | -3.43 | -3.13 | -1.23 | -0.92 | -0.31 | |
| 500 | -3.98 | -3.42 | -3.13 | -1.24 | -0.93 | -0.32 | |
| >500 | -3.96 | -3.41 | -3.12 | -1.25 | -0.94 | -0.33 |
Por exemplo, se o valor obtido para 50 observações com tendência (caso C) for de -4.57, ao comparar com a tabela, observa-se que é mais negativo que -3.50. Então, no nível de 95% a hipótese nula de uma raiz unitária será rejeitada, ou seja, é pouco provável possuir uma raiz e portanto pouco provável ser estacionário.
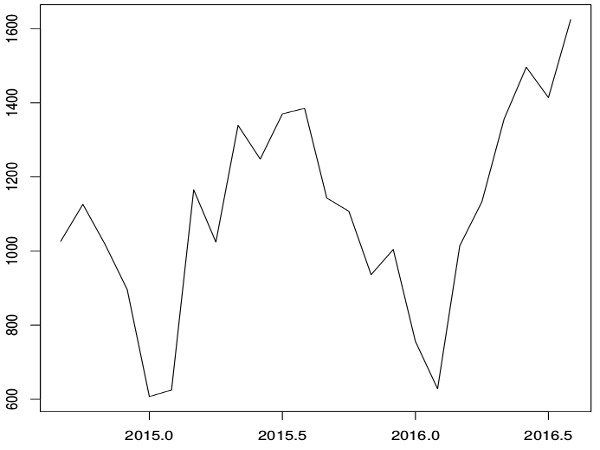
Outro exemplo, utilizando os dados da série temporal do exemplo A: considerando o mesmo valor de n, caso o valor do teste for de 0.23 no caso B, têm-se no nível entre 1% e 5% de que a hipótese nula seja rejeitada, ou seja, como é pouco provável rejeitar a hipótese nula, é muito provável existir uma raiz unitária e portanto é muito provável ser um processo estacionário.
O teste de Phillips-Perron (PP) é uma generalização do teste de Dickley-Fuller para os casos em que os erros são correlacionados e, possivelmente, heterocedásticos.
O teste KPSS (criado por Denis Kwiatkowski , Peter C. B. Phillips, Peter Schmidt e Yongcheol Shin) possui hipóteses diferentes dos testes anteriores:
- H0: “A série é estacionária”
- H1: “A série apresenta raiz unitária”
Além disso, a ausência de uma raiz unitária não é uma prova de estacionariedade, e sim de que possui uma tendência somente em função do tempo que pode ser removida para restar apenas um processo estacionário.
Supondo que seja possível decompor a série em componentes de tendência, passeio aleatório e erro, considerando seus resíduos em uma regressão, é possível determinar um estimador para a variância dos erros nesta regressão.
A função ur.kpss() realiza o cálculo dessa estatística. Ela recebe os parâmetros “type” com o tipo da parte determinística (constante “mu” ou constante com tendência “tau”) e opcionalmente “lags”, com o número máximo de defasagens usadas para a correção do termo de erro: “short”, “long” ou “nil” (sem correção de erro). Utilizando o comando dentro das funções print(summary()), são impressos na tela mais detalhes e o valor da estatística.
Aqui também existe uma tabela com os valores críticos para o teste KPSS, considerando os valores para mu e tau – fonte:
| 1% | 2.5% | 5% | 10% | |
|---|---|---|---|---|
| mu | 0.739 | 0.574 | 0.463 | 0.347 |
| tau | 0.216 | 0.176 | 0.146 | 0.119 |
Por exemplo, considerando o caso “tau” e valor da estatística em 0.3544, este é maior que os valores críticos tabelados para esse caso. Assim, deve-se rejeitar a hipótese nula, ou seja, é pouco provável a série ser estacionária.
Voltando à série temporal do exemplo A: para o caso mu e valor de teste 0.2203, como é menor que os valores tabelados, não se deve rejeitar a hipótese nula, ou seja, é muito provável que a série seja estacionária.
Note que, em todos os testes, deve-se saber se existe tendência – veja mais sobre esse tópico clicando no link.
Transformação
A maioria dos procedimentos de análise estatística de séries temporais supõe que estas sejam estacionárias. Assim, será necessário transformar os dados originais se estes não formam uma série estacionária. A transformação mais comum consiste em tomar diferenças sucessivas da série original, até se obter uma série estacionária – geralmente uma ou duas diferenças são suficientes. Esse procedimento é normalmente utilizado para remover tendências.
Uma primeira diferença é definida com a subtração entre o valor em um momento e no momento anterior. Se um processo for estacionário de segunda ordem, ele será dito estritamente estacionário. A n-ésima diferença de uma série temporal Z(t) é:
![]()
Para tornar a série estacionária deve-se tomar diferenças quantas vezes for necessário, até atingir estacionariedade – são chamadas de séries não estacionárias homogêneas. Um modelo é estacionário se, para todo t, tem-se os valores de média, variância e covariâncias constantes. Por exemplo, quando a série oscila ao redor de um nível e salta para outro, basta uma diferença para torná-la estacionária; se a série oscila em uma direção e depois muda, são necessárias duas diferenças para ficar estacionária.
No R, uma ou mais diferenças podem ser realizadas através da função diff(). Como argumentos, usar a série temporal, mas é possível também definir o número de diferenças (parâmetro “differences”) e o lag (parâmetro “lags”) – o padrão é usar uma diferença e lag igual a 1. Conforme a opção de modelo utilizado, esse cálculo de diferenças já está incluso como um parâmetro de entrada da função que calcula o modelo (por exemplo, a função Arima do pacote forecast recebe os parâmetros p, d e q, referentes à auto-regressão, diferenças e médias móveis, respectivamente).
Modelos
Para tentar representar os dados através de uma função matemática, existem os modelos paramétricos para séries temporais, ou seja, modelos que o número de parâmetros é finito. Os mais frequentemente usados são os modelos de erro (ou de regressão), os modelos autorregressivos e de médias móveis (ARMA) e os modelos autorregressivos integrados e de médias móveis (ARIMA). A função de autocorrelação é utilizada para identificarmos um modelo adequado para a série temporal – veja mais no post sobre modelo ARIMA.
Fontes




Como podemos decidir se um teste Dickey-Fuller Aumentado apresentar resultados contraditórios ao teste Phillips-Perron?
Oi Breno,
Eu olharia para o tipo dos erros para escolher um. Geralmente, o teste Adf é usado quando os erros são homocedásticos e o teste PP, para erros heteroscedásticos.