Dado um conjunto de amostras, uma forma de quantificar a incerteza na escolha de um evento é através da probabilidade P(A) do evento A acontecer. Caso esse evento ocorra dando informações sobre outro evento B, é dito que eles são dependentes – caso contrário, são A e B são eventos independentes.
Matematicamente, a probabilidades de dois eventos independentes acontecer é calculada multiplicando-se as probabilidades individuais de cada um. Por exemplo, a probabilidade de cair cara duas vezes seguidas na moeda é dada pelo produto das duas (se fosse cara em uma das duas, seria a soma delas):
\(
P(A\cap B) = P(A)\cdot P(B) = \frac{1}{2}\cdot\frac{1}{2} = \frac{1}{4}
\)
No caso em que o evento A está condicionado ao evento B, por exemplo, é dito que A e B são eventos dependentes. Ou seja, uma vez que conhecemos o evento A, sabemos que B acontece. Considerando que A seja obter ímpar jogando um dado e B seja cair um número menor que 3, essa probabilidade é calculada por:
\(
P(A|B) = \frac{P(A\cap B)}{P(B)} = \frac{|\{1,3,5\}\cap\{1,2,3\}|}{|\{1,2,3\}|} = \frac{|\{1,3\}|}{|\{1,2,3\}|} = \frac{2}{3}
\)
É possível usar as teorias envolvendo conjuntos (complementariedade, subconjuntos, etc) para contar quantos elementos estão na intersecção e calcular a probabilidade condicional. Por exemplo, considerando duas moedas, qual seria a probabilidade do evento “duas moedas são caras” (A) ser condicionada pelo evento “a moeda da direita é cara” (B)?
Note que a probabilidade das duas moedas serem cara existe dentro da probabilidade da moeda da direita ser cara (A ⊂ B). Usando a probabilidade condicional, tem-se que:
\(
P(A|B) = \frac{P(A)}{P(B)} = \frac{\frac{1}{4}}{\frac{1}{2}} = \frac{1}{2}
\)
Já no caso de condicionar o mesmo evento A ao evento “ao menos uma das moedas é cara” (C), a probabilidade P(C) é a soma das probabilidades de “uma cara e uma coroa” e “duas caras”, ou seja, 1/2 + 1/4 = 3/4, e a probabilidade final é:
\(
P(A|C) = \frac{P(A)}{P(C)} = \frac{\frac{1}{4}}{\frac{3}{4}} = \frac{1}{3}
\)
A Cadeia Condicional de probabilidade permite dividir a probabilidade de um evento usando a probabilidade condicional. Ou seja, pode-se fazer um diagrama vertical onde cada linha acrescentada inclui todas as possibilidades para cada evento.
Teorema de Bayes
O Teorema de Bayes relaciona probabilidades marginais (variáveis contidas no subconjunto) e probabilidades condicionais (que depende de uma dada condição). Através da “regra de Bayes”, é possível saber a probabilidade P(A|B) quando se conhece apenas a probabilidade de P(B|A), conforme segue:
\(
P(A|B) = \frac{P(A\cap B)}{P(B)} = \frac{P(B\cap A)}{P(B)} = \frac{P(B|A)\cdot P(A)}{P(B)}
\)
O objetivo aqui é responder à seguinte questão: qual é a probabilidade de que o evento A tenha ocorrido, visto que o evento B acabou de ocorrer? Essa probabilidade é simbolizada por P(A∣B). P(A) e P(B) são as probabilidades a priori (ou marginais) de A e B, ou seja, o que já se conhece antes de implementar a condição com um novo conhecimento sobre a situação. Essa condição de novas evidências implica em novas probabilidades, conhecidas como probabilidades a posteriori (ou condicionais): P(A|B) e P(B|A), que é a probabilidade de observar B dada a ocorrência de A (indica a compatibilidade dos elementos com a hipótese/evento A dado).
Pode-se generalizar a fórmula para mais de um evento A. Considere os eventos A1, A2, … , Ak mutuamente exclusivos, cuja união é todo o espaço amostral de um experimento, e o evento B com probabilidade diferente de zero:
\(P(A_i|B)=\frac{P(B|A_i)\cdot P(A_i)}{\sum\limits_{x=1}^{k}P(B|A_x)\cdot P(A_x)}\)
Assim, cada análise compõe-se de dois tipos de informações: os dados que estão sendo analisados e a informação prévia. O pesquisador é livre para escolher qualquer informação prévia que ajuda a explicar os dados que estão sendo analisados. Por exemplo, no caso de fazer uma previsão de chuva, pode-se utilizar o resultado de outra pesquisa dizendo que o modelo numérico acerta 86% dos casos como um “peso” para calcular a probabilidade de chuva.
Aplicação
Suponha uma doença D e seu teste T com as seguintes características (lembrando que o ~ é complementar ou negação):
- A doença afeta 1 em cada 10 mil pessoa: P(D) = 1/10000 = 0.0001
- A probabilidade do teste dar um falso positivo (dar positivo, sendo que a pessoa não possui a doença) é de 2%: P(T|~D) = 0.02
- A probabilidade do teste dar um falso negativo (dar negativo, sendo que a pessoa possui a doença) é de 1%: P(~T|D) = 0.01
Se uma pessoa fizer o teste da doença e der positivo, qual é a probabilidade de que a pessoa tenha a doença? Ou seja, qual é o valor de P(D|T) – probabilidade de que o evento D tenha ocorrido, visto que o evento T ocorreu?
Considerando a definição de probabilidade condicional, complementariedade e o Teorema de Bayes (aproximadamente nessa ordem), P(D|T) deve ser reescrita em função das probabilidades existentes:
\(
P(D|T) = \frac{P(D\cap T)}{P(T)} =\\
= \frac{P(D\cap T)}{P(T\cap D) + P(T\cap ~D)} =\\
= \frac{P(T|D)\cdot P(D)}{(P(T|D)\cdot P(D)) + P(T|~D)\cdot P(~D)} =\\
= \frac{(1 – P(~T|D))\cdot P(D)}{((1 – P(~T|D)\cdot P(D)) + (P(T|~D)\cdot P(~D)} =\\
= \frac{(1-0,01)\cdot(0,0001)}{((1-0,01)\cdot 0,0001) + ((0,02)\cdot (1-0,0001))} =\\
P(D|T) \approx 0,0049
\)
Assim, menos que 0,5% das pessoas obtiveram o teste com resultado positivo e possuem a doença. Como é esperado que 1 em cada 10 mil pessoas tenha a doença, em uma população de 10 milhões de habitantes, mil delas ficarão doentes. Dessas 1000 pessoas, 999 (0,5% da população) terão o resultado do teste como positivo (verdadeiro positivo). Das pessoas que não ficaram doentes (9.999.000), espera-se que 99.990 de seus testes resultem em positivo (falso positivo).
Rede Bayesiana
As redes Bayesianas são grafos que representam relações de probabilidade condicional, ou seja, como que a ocorrência de certas variáveis depende do estado de outra. Um modelo gráfico probabilístico que expressa essas dependências condicionais entre variáveis aleatórias por meio de arcos é conhecido como DAG (do inglês, grafo acíclico direcionado).
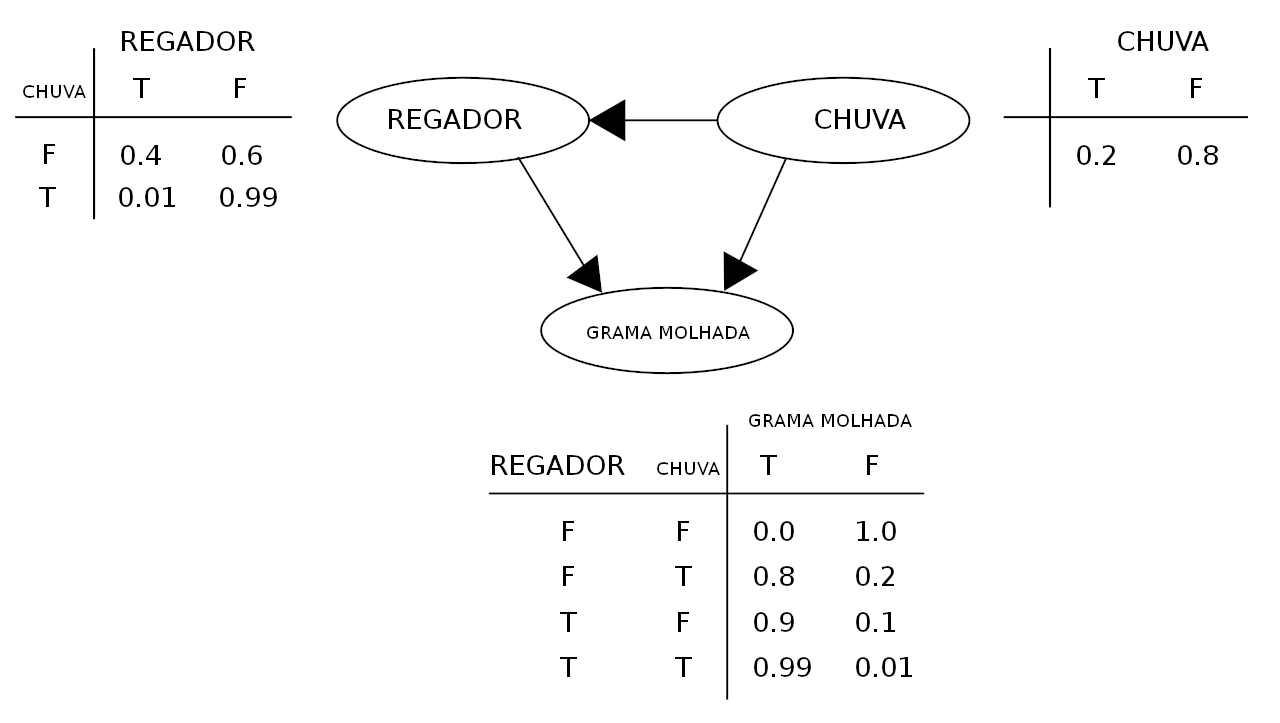
Veja esse exemplo de modelagem usando rede Bayesiana: considere um sistema em que a chuva molhe a grama (G = grama molhada) e o regador (R = regador ligado) somente seja acionado quando não chover (C = chovendo). Considerando que cada variável admite somente V (Verdadeiro) ou F (Falso), a distribuição de probabilidade conjunta é:
\(
P(G, R, C) = P(G|R,C)\cdot P(R|C)\cdot P(C) [1]
\)
Qual é a probabilidade que esteja chovendo, dado que a grama está molhada? Usando a fórmula da probabilidade condicional:
\(
P(C = V|G = V) = \frac{P(G = V \cap C = V)}{P(G = V)} = \frac{\sum P(G = V,R,C = V)}{\sum P(G = V,R,C)} [2]
\)
Utilizando a expansão para a probabilidade conjunta (eq. 1) e os valores das probabilidades condicionais apresentadas no diagrama, os valores podem ser substituídos na fórmula da probabilidade condicional (eq. 2), obtendo-se o valor de 35,77% de probabilidade para que esteja chovendo, considerando-se que a grama esteja molhada.
É possível trabalhar com variáveis contínuas, em vez de discretas. Nesse caso, são usadas densidades de probabilidades. Ou também partir de variáveis qualitativas para construir estimativas numéricas. O Teorema de Bayes permite, desde que identificado o seu limite de conhecimento, estipular probabilidades de outras explicações para um certo fenômeno. Conforme for agregando conhecimento com novas informações, é possível melhorar as estimativas de probabilidades de cada explicação para ficar cada vez menos errado – ou seja, uma técnica de gestão de erros.
“No momento que você perde inocência sobre alguma coisa, você adquire responsabilidade. Se você não assumir a responsabilidade, você está sendo irresponsável (…) e o Teorema de Bayes é uma ferramenta muito útil se você está preocupado em começar a assumir as responsabilidades. O problema é que ele não é tão convidativo em um mundo onde as pessoas não querem assumir responsabilidades. Elas querem sempre um guru que vai dizer pra elas que qualquer problema da sua vida vai ter um responsável que não é você. Porque você entender que é o responsável pela sua vida, pelas suas decisões é duro demais.”
Roberto Spinelli (Pena)
Veja também uma aplicação do Teorema de Bayes no problema de Monty Hall (Porta dos Desesperados) clicando no link.
Fontes



2 comments