Perceptron – redes neurais

As Redes Neurais Artificiais (RNAs) são modelos computacionais inspirados no sistema nervoso central, ou seja, capazes de realizar o aprendizado de máquina (machine learning) e reconhecimento de padrões. O tipo mais simples de rede neural artificial foi proposto em 1958 por Frank Rosenblatt, conhecido como perceptron. A palavra em latim para o verbo compreender é “percipio“, e sua forma supina é “perceptum”, ou seja, a rede deve ser capaz de compreender o mundo exterior. Esse algoritmo de aprendizagem supervisionada considera um período de treinamento (com valores de entrada e saída) para definir se uma nova entrada pertence a alguma classe específica ou não.

Mark I Perceptron. Foto: Cornell Aeronautical Laboratory

O Mark I Perceptron foi uma máquina projetada para reconhecimento de imagem e foi a primeira implementação do algoritmo. Tinha uma matriz de 400 fotocélulas, conectadas aleatoriamente aos “neurônios”. Os pesos foram codificados em potenciômetros, e as atualizações de peso durante a aprendizagem eram realizadas por motores elétricos. Atualmente, o algoritmo pode ser implantado em qualquer computador usando diversas linguagens de programação.

O Perceptron é um classificador linear, ou seja, os problemas solucionados por ele devem ser linearmente separáveis. O gráfico a seguir mostra um conjunto de pontos bi-dimensional que pode ser separado linearmente – note que é possível passar uma linha reta entre os dois grupos de cores diferentes:

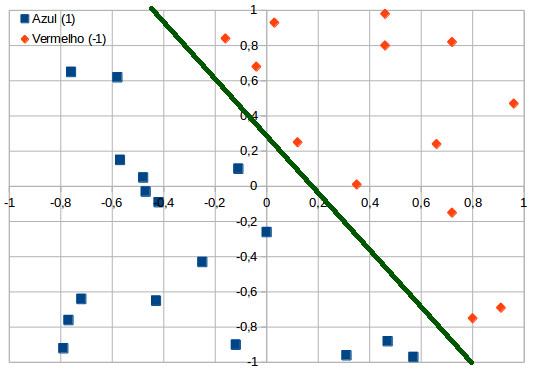
Gráfico com problema linearmente separável em duas dimensões

A separação entre as duas classe está representada por uma reta, já que é um gráfico de duas dimensões – se fossem três dimensões, seria um plano; 4 dimensões ou mais, seria um hiperplano. Ainda no gráfico, a reta define o limite entre duas regiões, por isso é chamada de função limiar. Essa função é responsável por determinar a forma e a intensidade de alteração dos valores transmitidos de um neurônio a outro. A UTCS possui uma versão online desse problema, na qual é possível incluir pontos vermelhos e azuis, recalculando-se automaticamente a melhor reta para separar os conjuntos e depois apresentando a classificação pelo algoritmo pressionando os botões “train” e “classify”.

Agora imagine se existissem dois pontos vermelhos, um em (-1,-1) e outro em (1,1), e dois azuis, um em (-1,1) e outro em (1,-1). Não teria como passar uma linha reta dividindo o gráfico em duas regiões. Esse é conhecido como “problema XOR” (“ou exclusivo”), sendo que XOR é uma operação lógica entre dois operandos que resulta em um valor lógico verdadeiro se e somente se exatamente um dos operandos possui valor verdadeiro. Esse problema pode ser solucionado com a criação de uma camada intermediária em uma rede com dois neurônios e graficamente com uma estrutura em três (ou mais) dimensões. Desse modo, é possível o uso de funções não-lineares. Veja mais no post sobre Redes Neurais Artificiais.

Algoritmo

Um neurônio recebe um impulso através dos dendritos, processa o sinal e dispara um segundo impulso, que produz uma substância neurotransmissora que flui do corpo celular para o axônio, e então para outro neurônio.

Esquemas de neurônios natural e artificial

Uma analogia pode ser feita para criar um “neurônio artificial”:

Os sinais de entrada {x1, x2, xn} são ponderados/multiplicados por {w1, w2, wn}
A função agregadora {Σ} recebe todos os sinais e realiza a soma dos produtos dos sinais
Ao resultado, é somado o limiar de ativação {Θ} (também chamado de bias ou parâmetro polarizador), soma essa conhecida como potencial de ativação {u}; o bias é uma constante que serve para aumentar ou diminuir a entrada líquida u, de forma a transladar a função de ativação no eixo de u
Obs.: o bias pode ser tratado como “mais um peso”, o que na prática envolve acrescentar uma nova entrada do tipo x_k0 = 1 com um peso associado w_k0.
A função de ativação {g} é aplicada sobre o potencial de ativação {u} para deixar o sinal passar ou não

Todas as saídas da rede são trocadas no início de intervalos discretos chamados de época. No início de cada época, a soma das entradas de cada neurônio é somado e aplicada a função de ativação. Essa função de ativação pode ser uma função bipolar (somente dois valores de saída), uma reta (função linear) ou até uma função gaussiana, hiperbólica, etc. No caso de uma função bipolar, pode-se considerar a saída igual a “1” se o valor de u (somatório dos produtos) for maior ou igual a 0 e “-1” no caso de u < 0.

O processo de treinamento tem como objetivo calibrar os pesos de modo iterativo, partindo de valores aleatórios (geralmente entre 0 e 1). A taxa de aprendizagem {η} (também um valor entre 0 e 1) diz o quão rápido a rede chega ao seu processo de classificação: um valor muito pequeno causa demora a convergir, enquanto que um valor muito alto pode levar para valores fora do ajuste e nunca convergir.

Assim, o vetor contendo os pesos de um passo de iteração será o resultado da soma de si mesmo no passo anterior com o produto das seguintes parcelas: a taxa de aprendizagem, a amostra de aprendizagem desse passo e a diferença entre o valor desejado (saída “certa”) para esse passo e o valor de saída produzido pela rede (passo 6.2.3.1 do algoritmo abaixo). Essa diferença é chamada de erro de saída: se for diferente de zero, é aplicada a correção.

Juntando tudo, veja como fica o algoritmo da fase de treinamento:

Obter o conjunto de amostras de treinamento {x^(k)}
Associar o valor desejado {d^(k)} para cada amostra obtida
Iniciar o vetor de pesos {w} com valores aleatórios pequenos
Especificar a taxa de aprendizagem {η}
Iniciar o contador de número de épocas (época = 0)
Repetir as seguintes instruções até que o erro de saída inexista:
6.1 Inicializa erro (erro = “inexiste”)
6.2 Fazer o seguinte loop para todas as amostras de treinamento {x^(k), d^(k)}:
6.2.1 u = w^T.x^(k) 6.2.2 y = g(u)
6.2.3 Se o erro existir (y diferente de d^(k)):
6.2.3.1 w = w + η.x^(k).(d^(k)-y)
6.2.3.2 Atualiza condição de erro (erro = “existe”)
6.3 Atualiza contador de épocas (época = época + 1)

Após o treinamento, entra o algoritmo de operação para gerar novos valores:

Obter o conjunto de amostras a serem classificadas
Carregar o vetor de pesos {w} ajustado no treinamento
Para cada amostra {x}:
3.1 u = w^T.x
3.2 y = g(u)
3.3 Verificar saída
3.3.1 Se y = -1, amostra {x} pertence à {classe A}
3.3.2 Se y = 1, amostra {x} pertence à {classe B}

Com isso, as novas amostras devem ser classificadas em uma das duas classes com base em classificações realizadas no período de treinamento.

Implementação em Python

No script apresentado a seguir, todas as funções estão contidas na classe “perceptron”, cuja descrição segue em comentário acima do código. Nela estão definidas a taxa de aprendizagem, o número máximo de épocas e o limiar de ativação (taxa_aprendizado=0.1, epocas=1000, limiar=1) por padrão, caso o usuário não passe um valor específico. O limiar/bias é incluído no início das listas “amostras” e “pesos” (ou seja, iserido em cada amostra e cada peso), de modo a incluir o bias na somatória.

#!/usr/bin/python
# -*- coding: utf-8 -*-
# Implementação Perceptron

import sys
import random

class Perceptron:

	## Primeira função de uma classe (método construtor de objetos)
	## self é um parâmetro obrigatório que receberá a instância criada
	def __init__(self, amostras, saidas, taxa_aprendizado=0.1, epocas=1000, limiar=1):
		self.amostras = amostras
		self.saidas = saidas
		self.taxa_aprendizado = taxa_aprendizado
		self.epocas = epocas
		self.limiar = limiar
		self.n_amostras = len(amostras) # número de linhas (amostras)
		self.n_atributos = len(amostras[0]) # número de colunas (atributos)
		self.pesos = []

	## Treinamento para amostras "antigas"
	def treinar(self):

		# Inserir o valor do limiar na posição "0" para cada amostra da lista "amostras"
		# Ex.: [[0.72, 0.82], ...] vira [[1, 0.72, 0.82], ...]
		for amostra in self.amostras:
			amostra.insert(0, self.limiar)

		# Gerar valores randômicos entre 0 e 1 (pesos) conforme o número de atributos
		for i in range(self.n_atributos):
			self.pesos.append(random.random())
		# Inserir o valor do limiar na posição "0" do vetor de pesos
		self.pesos.insert(0, self.limiar)
		
		# Inicializar contador de épocas
		n_epocas = 0

		while True:
			# Inicializar variável erro
			# (quando terminar loop e erro continuar False, é pq não tem mais diferença entre valor calculado e desejado)
			erro = False

			# Para cada amostra...
			for i in range(self.n_amostras):
				# Inicializar potencial de ativação
				u = 0
				# Para cada atributo...
				for j in range(self.n_atributos + 1):
					# Multiplicar amostra e seu peso e também somar com o potencial que já tinha
					u += self.pesos[j] * self.amostras[i][j]
				# Obter a saída da rede considerando g a função sinal
				y = self.sinal(u)

				# Verificar se a saída da rede é diferente da saída desejada
				if y != self.saidas[i]:
					# Calcular o erro
					erro_aux = self.saidas[i] - y
					# Fazer o ajuste dos pesos para cada elemento da amostra
					for j in range(self.n_atributos + 1):
						self.pesos[j] = self.pesos[j] + self.taxa_aprendizado * erro_aux * self.amostras[i][j]
					# Atualizar variável erro, já que erro é diferente de zero (existe)
					erro = True

			# Atualizar contador de épocas
			n_epocas += 1

			# Critérios de parada do loop: erro inexistente ou o número de épocas ultrapassar limite pré-estabelecido
			if not erro or n_epocas &gt; self.epocas:
				break

	## Testes para "novas" amostras
	def teste(self, amostra):
		# Inserir o valor do limiar na posição "0" para cada amostra da lista "amostras"
		amostra.insert(0, self.limiar)
		# Inicializar potencial de ativação
		u = 0
		# Para cada atributo...
		for i in range(self.n_atributos + 1):
			# Multiplicar amostra e seu peso e também somar com o potencial que já tinha
			u += self.pesos[i] * amostra[i]
		# Obter a saída da rede considerando g a função sinal
		y = self.sinal(u)
		print('Classe: %d' % y)

	## Função sinal
	def sinal(self, u):
		if u &gt;= 0:
			return 1
		return -1

# Amostras (entrada e saída) para treinamento
amostras = [[0.72, 0.82],   [0.91, -0.69],
			[0.46, 0.80],   [0.03, 0.93],
			[0.12, 0.25],   [0.96, 0.47],
			[0.8, -0.75],   [0.46, 0.98],
			[0.66, 0.24],   [0.72, -0.15],
			[0.35, 0.01],   [-0.16, 0.84],
			[-0.04, 0.68],  [-0.11, 0.1],
			[0.31, -0.96],  [0.0, -0.26],
			[-0.43, -0.65], [0.57, -0.97],
			[-0.47, -0.03], [-0.72, -0.64],
			[-0.57, 0.15],  [-0.25, -0.43],
			[0.47, -0.88],  [-0.12, -0.9],
			[-0.58, 0.62],  [-0.48, 0.05],
			[-0.79, -0.92], [-0.42, -0.09],
			[-0.76, 0.65],  [-0.77, -0.76]]

saidas = [-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]

# Chamar classe e fazer treinamento
rede = Perceptron(amostras, saidas)
rede.treinar()

# Entrando com amostra para teste
rede.teste([0.46, 0.80])
#sys.exit("fim de teste")

Os dados utilizados correspondem a pares de coordenadas (x,y) para classificação de cores: 1 é azul e -1 é vermelho. No caso do ponto utilizado como teste (terceira amostra), ele deve imprimir “Classe: -1” ao rodar o script.

Fontes

Curso Machine Learning e Data Science com Python – Marcos Castro & Gileno Alves Santa Cruz Filho
Introduzindo Redes Neurais e Perceptron – Marcel Caraciolo
Introdução às Redes Neurais Artificiais – André Cardon & Daniel Nehme Müller (UFRGS, 1994)
Soluções de Equações Diferenciais Usando Redes Neurais de Múltiplas camadas com os métodos da Descida mais íngreme e Levenberg-Marquardt – Brigida Cristina Fernandes Batista (UFPA, 2012)
Redes Neurais – José Gomes de Carvalho Jr. (UFF)
CoteiaWIKI
Wikipedia – Perceptron