O livro “O Sinal e o Ruído – Por que Tantas Previsões Falham e Outras não” (“The Signal and The Noise”) foi escrito pelo estatístico americano Nate Silver (1978-) e publicado em 2013. Com um número cada vez maior de dados para analisar, o autor ressalta no livro que todos os modelos são falhos e que muita informação também pode trazer muito ruído, gerando más previsões.
O artigo “A Mathematical Theory of Communication”, escrito por Claude Shannon (1916-2001) e publicado em 1948, lançou as bases da teoria matemática da informação. Dentre os conceitos que vieram à tona, estão o de sinal, sequência de estados em um sistema de comunicação que codifica uma mensagem, e de ruído, responsável por distorcer o significado da mensagem original.
“Todos os modelos estão errado, mas alguns são úteis.”
George E. P. Box (estatístico britânico, 1919-2013)
A frase acima afirma que todos os modelos são simplificações da realidade. O melhor modelo de um gato é um gato, ou seja, sempre será excluído algum detalhe. O quão importante é cada detalhe depende do problema a ser tratado, do grau de precisão exigido como resposta e do custo em fazer a modelagem e a previsão.
“Os seres humanos têm uma enorme capacidade de ignorar os riscos que ameaçam seu medo de vida, como se essas ameaças se afastassem.”
A frase acima está no contexto dos questionamentos em como ninguém teria previsto o estouro da bolha imobiliária nos EUA e a consequente crise de 2008. Nosso cérebro gera nossas certezas “absolutas” de acordo com o que nos agrada. Um pouco desse comportamento pelas pessoa é compreensível pela questão do conforto cognitivo, explicado no post sobre o livro Pensando rápido e devagar. Mas também chama atenção para encontrar um sinal no meio a um mar de informações ruidosas.
Em estatística, o nome dado ao ato de tomar um ruído como sinal é overfitting (sobreajuste). Nesse caso, o modelo fica tão bem ajustado aos dados, que só funciona para essa situação bem específica. Como o cenário para previsão é diferente do modelado, as previsões serão ruins.
Dentre os exemplos trabalhados no livro, estão a crise do subprime americano que estourou em 2007, comparar previsões de analistas e de modelos, medição de desempenho de jogadores em baseball, jogos de pôquer, previsão de terremotos, máquinas ganhando jogos de xadrez contra humanos e mercado financeiro.
Sobre modelagem do avanço de doenças, o autor levanta um ponto interessante sobre o diagnóstico de doenças. Quando problemas de saúde são amplamente discutidos na mídia, as pessoas ficam mais propensas a identificar seus sintomas e os médicos, a diagnosticá-los. Ele cita o exemplo do autismo, que não é doença, mas que teve um aumento de diagnósticos diretamente proporcional à frequência com que o termo autismo era usado em jornais dos EUA.
Quanto à modelagem de criminalidade, a forma de notificação pode influenciar as análises e previsões. Em Nova York, por exemplo, não é possível registrar boletins de ocorrência online, diferentemente de San Francisco. A maior facilidade em registrar as ocorrências colabora com que os índices de criminalidade em San Francisco tenham valores maiores.
Probabilidade condicional
Outro ponto interessante trazido pelo livro é a utilização do Teorema de Bayes para avaliar cenários. Nada muito útil surge em uma discussão entre pessoas que sustentam 0% ou 100% de possibilidade em relação a alguma coisa. A estatística Bayesiana fundamenta-se na probabilidade condicional, ou seja, na chance de uma hipótese ser verdadeira se tiver acontecido determinado evento.
O primeiro passo é estimar a probabilidade de um evento A numa condição que a hipóteses seja verdadeira. Depois, estimar a probabilidade desse mesmo evento em uma condição em que a hipótese seja falsa. Por fim, estimar a probabilidade prévia – chute inicial ou uma probabilidade empírica. Veja o exemplo a seguir que consta do livro, a respeito da probabilidade de um avião (ou mais) atingir um prédio em um ataque terrorista:
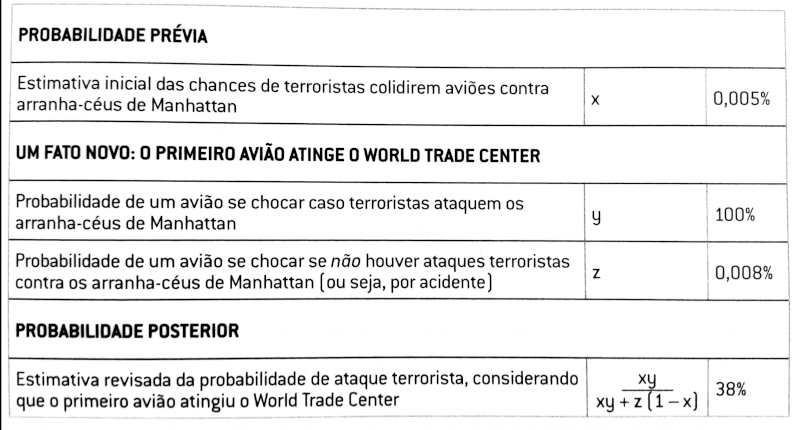
A ideia é repetir o processo à medida que tivermos novos indícios. Nesse exemplo, a probabilidade prévia pode ser alterada para o valor descoberto na tabela e gerar uma nova probabilidade de um novo atentado. Nesse caso, a nova probabilidade posterior seria de 99,99%.
Previsão de tempo
Apesar dos cientistas conhecerem boa parte das equações a serem resolvidas na previsão de tempo, a computação ainda está longe de calculá-las para cada molécula na atmosfera da Terra. Por isso, são feitas algumas aproximações. Além disso, depois do trabalho de Edward Lorenz “A batida das asas de uma borboleta no Brasil pode provocar um tornado no Texas?” (1972), tornou-se clara a não linearidade de movimentos atmosféricos.
A sensibilidade às condições iniciais é outra característica desse e outros sistemas caóticos. Pequenas mudanças são introduzidas para representar a incerteza inerente na qualidade dos dados obtidos através de observações. Desse modo, algumas previsões determinísticas são agrupadas em uma previsão probabilística. Por exemplo, se existe 40% de chance de chover amanhã, podemos entender que em 40% de suas simulações apareceu precipitação naquele ponto previsto, enquanto em outras, não – veja mais no post O que é probabilidade de chuva?
Para qualquer previsão do tempo, ela precisa ser melhor do que duas coisas:
- Persistência, ou seja, o pressuposto de que o tempo no dia seguinte será o mesmo que foi hoje;
- Climatologia (média histórica, de longo prazo) das condições na data e área especificadas.
Se não for possível aperfeiçoar o modelo de previsão do tempo para passar nesse teste na maioria das vezes, de nada adianta o uso de um grande poder computacional para rodá-lo.
Quanto mais “pra frente” for a previsão, os modelos tendem a ser menos precisos. No livro, é dito que previsões comerciais feitas com até oito dias de antecedência são melhores que a climatologia ou a persistência. Depois disso, quem vence é a climatologia.
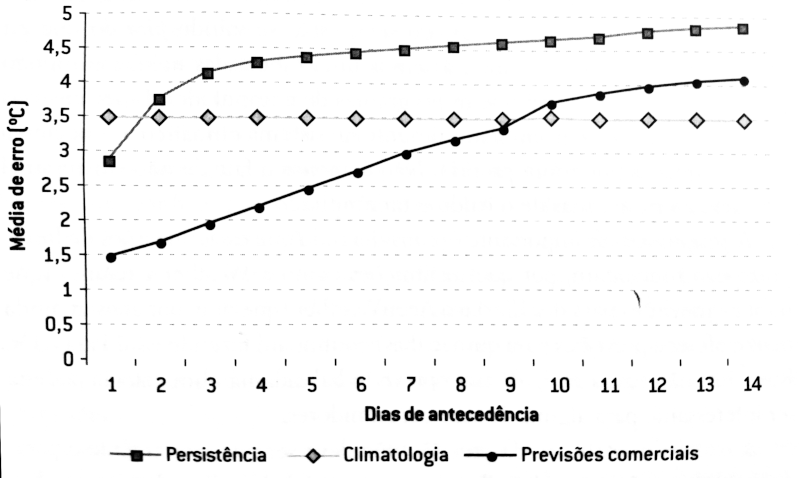
Por tudo o que foi dito até aqui, note que erros de modelos são inevitáveis. Talvez o computador tenha tendência conservadora em prever uma precipitação noturna em um ponto ou não saiba que a neblina em outro local desaparece após o nascer do sol se o vento estiver soprando de tal direção, mas pode durar mais se vier de uma região mais úmida. Essas distinções são compiladas ao longo do tempo pelos meteorologistas que percebem as falhas dos modelos frente a seu conhecimento sobre a atmosfera.