O Sol é formado por gás ionizado, cuja energia é gerada pela fusão nuclear de seus elementos constituintes. O post Como é gerada a energia no Sol explica melhor a formação da energia solar e o post Radiação solar na Terra mostra como a energia vinda do Sol atinge nosso planeta e interage com suas primeiras camadas. Nesse texto, o objetivo é calcular a energia solar que atinge a atmosfera terrestre, antes de interagir com seus constituintes.

O Sol emite energia radiante, medida em Joules, cujo fluxo em função do tempo é medido em Watts. Quando esse fluxo atravessa uma determinada área, é chamado de irradiância. Ou seja, a irradiância num certo ponto de uma superfície é definido como a razão entre o fluxo de radiação e a área do elemento de superfície, cuja unidade é W/m².
A irradiância do Sol, integrada em todo o espectro eletromagnético, à distância média Terra-Sol é denominada irradiância solar total (ou constante solar \(\epsilon _0\)). Considerando-se uma superfície perpendicular à direção do feixe incidente no topo da atmosfera, seu valor médio é de 1367 W/m². O topo da atmosfera é definida teoricamente como a altitude acima da qual não ocorre interação significativa entre a radiação eletromagnética e os constituintes atmosféricos.
Desconsiderando-se variações da própria atividade solar, que pode atuar em escalas de tempo de minutos até anos, pode-se incluir os efeitos mais previsíveis relacionados aos ciclos anuais do Sol. Dentre esses ciclos, estão:
- variação da distância Terra-Sol, devido à orbita elíptica em seu movimento de translação ao redor do Sol;
- variação da declinação solar, que é a inclinação do eixo de rotação da Terra com relação à normal ao plano da eclíptica;
- ciclo diurno, devido à rotação da Terra em torno de seu próprio eixo.
A distância solar média entre a Terra e o Sol é a definição de 1 UA (unidade astronômica) e equivale a 149 597 870 km. No entanto, essa distância corresponde a 0,983 UA no periélio (em torno de 3 de janeiro) e 1,017 UA no afélio (em torno de 4 de julho). Já a declinação solar vale da ordem de 23,5° no solstício (de inverno ou verão, conforme o hemisfério) e 0° no equinócio (de outono ou primavera).
Um dia solar é o intervalo de tempo necessário para que o Sol complete um ciclo sobre um observador estacionário na Terra, o que não necessariamente tem a duração de 24 horas. Sua duração varia ao longo do ano e são possíveis discrepâncias de até 16 minutos. Esta discrepância é denominada equação do tempo e é medida com relação a um movimento terrestre perfeitamente uniforme. Essa equação é definida como a diferença entre o tempo solar verdadeiro (associado às condições reais da órbita da Terra em torno do Sol) e o tempo solar médio local (associado à noção de um dia solar médio, com duração exata de 24 horas).
Por sua vez, o tempo médio local pode ser definido em termos da hora UTC e da diferença de longitude com relação ao meridiano de Greenwich. Assim, pode-se definir o ângulo horário, em graus, em função da equação do tempo.
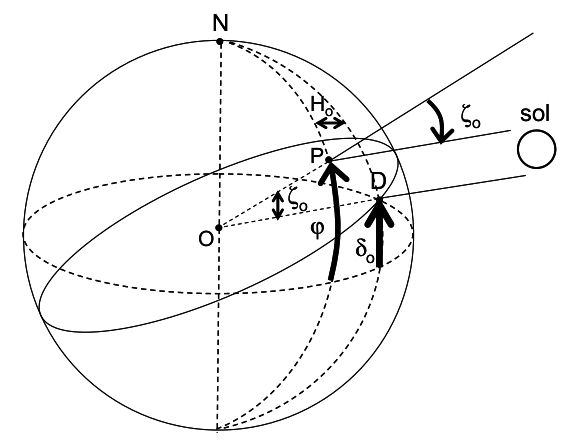
Na grande maioria dos códigos de transferência radiativa, a atmosfera é aproximada como sendo constituída por camadas plano-paralelas entre si. Dessa forma, para conhecer o valor da irradiância solar incidente sobre uma superfície horizontal no topo da atmosfera, é preciso conhecer também o ângulo zenital solar (ζ0 ou Z), formado entre os raios solares e a vertical local – o ângulo de elevação é o complemento do ângulo zenital. É usual trabalhar com o cosseno do ângulo zenital, que pode ser descrito em função da latitude local (φ ou lat), ângulo de declinação (δ0 ou dec) e do ângulo horário (H0, que está em função da longitude, da hora UTC e da equação do tempo). Assim, a fórmula para a irradiância solar \(\epsilon\) é:
\(\epsilon (d,Z)=\epsilon _0cos(Z)\left ( \frac{\bar{d}}{d} \right )\)
Sob a hipótese de que tais parâmetros não variam ao longo do dia, mas apenas de um dia para o outro, foram propostas fórmulas empíricas para o cálculo da equação do tempo (eqtime), da declinação (dec) e do termo relativo à distância Terra-Sol (d_astro). Todas estão contidas no script em python abaixo, em função do ângulo do dia (day_angle). Além delas, o script contém as fórmulas do cosseno do ângulo zenital (cosZ) e do ângulo horário (H0).
A função do código deve receber as seguintes variáveis: dia do ano (também chamado de dia juliano, que vai de 1 a 365), hora UTC, minutos, latitude e longitude (nessa ordem). Como saída, ela retorna distância Terra-Sol, cosseno e valor do ângulo zenital (em graus), nessa ordem. Por fim, o código calcula a irradiância no topo da atmosfera conforme a equação apresentada anteriormente.
- Código disponível no Github/ViniRoger – irradiance
Como exemplo, o script recebe 12 UTC das coordenadas de um local próximo a Brasília/DF (9h local) do dia do ano 214 (1 de agosto, se for ano bissexto, ou 2 de agosto caso contrário, conforme Day-Of-Year Calendar da NOAA). O código imprime na tela as três saídas da função principal e o valor da irradiância no TOA (Top Of Atmosphere) respectivos aos valores de entrada. No código, também está disponível uma implementação de modelo de céu claro, usando a biblioteca pvlib.
Cálculo derivados
A irradiância que atinge a superfície após interagir com a atmosfera, desconsiderando-se as nuvens, é chamada de irradiância de céu claro (ou CSI, do inglês Clear Sky Irradiance). Geralmente, esse valor é calculado através de Modelos de irradiância de céu claro – clique no link para saber mais. A CSI é definida como o produto entre a irradiância que atinge o topo da atmosfera e transmitância, conforme segue:
\(CSI=\tau\cdot G_{TOA}\)
Transmitância (\(\tau\)) é a fração do fluxo incidente sobre um sistema que consegue atravessá-lo. O conceito inclui tanto a transferência de radiação que não sofreu interação com o sistema quanto a produção de radiação difusa para o hemisfério de destino do fluxo incidente. É numericamente igual à soma da transmitância direta (associada apenas à atenuação do fluxo incidente) com a transmitância difusa (associada ao pró-espalhamento).
A determinação da irradiância em qualquer condição de nebulosidade é incluída em um modelo radiativo através do coeficiente de cobertura efetiva de nuvens (Ceff, Cloud cover index). Seu valor contém informações sobre a distribuição espacial e a espessura óptica das nuvens e é obtido a partir de imagens compostas claras e nubladas, produzidas por análise estatística de imagens de satélite. Seu cálculo é feito a partir da seguinte fórmula:
\(C_{eff}=\frac{L-L_{clr}}{L_{cld}-L_{clr}}\)
Onde L é a radiância medida, Lclr é a radiância de céu claro (mínimo de L no período, geralmente mensal) e Lcld é a radiância de céu totalmente encoberto (máximo de L no período, geralmente mensal). Quanto maior o valor da radiância medida, mais próxima ela esta da radiância de uma nuvem, e a razão, mais perto de 1; assim, quanto maior o valor do índice, maior a cobertura de nuvens.
O índice de claridade (Kt, Clearness Index) é uma medida da nitidez da atmosfera. Definido como a irradiância global horizontal (G) em superfície dividida pela mesma grandeza no topo da atmosfera (GTOA), é um número adimensional entre 0 (condições nubladas) e 1 (sem nuvens):
\(K_t=\frac{G}{G_{TOA}}\)
Em alguns lugares, o índice de claridade é definido em função da irradiância de céu claro, em vez da irradiância no topo da atmosfera, sendo identificado como K*:
\(K^*=\frac{G}{CSI}\)
Pode ser definido instantaneamente, a cada hora, diariamente ou mensalmente. Nesses casos de agrupar valores, deve-se somar as irradiâncias primeiro e depois fazer a razão entre os somatórios, já que a soma das razões não é a razão das somas. Isso equivale a fazer a média dos valores no numerador pela média dos valores no denominador, se o número de amostras de cada um for o mesmo.
Fontes
- YAMASOE, MARCIA AKEMI ; CORREA, M. P. . Processos Radiativos na Atmosfera – Fundamentos. 1. ed. São Paulo: Oficina de Textos, 2016. 142p .
- INPE – Glossário de Radiação Atmosférica

One comment