Manipulações de estatística

“As pessoas inventam estatísticas para provar qualquer coisa. 40% das pessoas sabem disso.” Essa frase de Homer Simpson ilustra bem o quanto estatísticas pode ser utilizadas para manipular as pessoas e esconder fatos. Aproveitando outra frase (mais séria), dita pelo escritor H. G. Wells, “o pensamento estatístico um dia será tão necessário para a cidadania eficiente quanto a capacidade de ler e escrever”. Esse post vai mostrar alguns exemplos que observei.

Apresentação dos números

“Em SP, 4 em cada 10 desistem de ação anticrack de Haddad”

Uma das matérias do jornal Folha de S. Paulo do dia 17/05/2015 tinha esse título. Longe de apoiar ou criticar o prefeito, mas note que os números afirmam que mais da metade dos viciados não desistem de ação anticrack. No entanto, do jeito que a manchete foi elaborada, parece o contrário, já que o destaque é dado ao que acontece com o menor número de viciados. Veja mais casos de manipulação da mídia clicando no artigo Podemos confiar nos noticiários?

O caso acima mostra a importância de um espírito crítico para não aceitar qualquer informação como verdadeira, inclusive se utilizar números como se eles se bastassem como atestado de verdade para o argumento. Para aprender mais sobre o uso da razão em nossas vidas, o livro “O mundo assombrado pelos demônios“, de Carl Sagan, é muito útil – clique no link para ver uma resenha dele.

Veja o exemplo dessa manchete: “Setor de serviços avança 0,1% em fevereiro e mostra dificuldade de recuperação, aponta IBGE”. No entanto, logo no início da matéria aparece o seguinte texto: “Em relação ao mesmo mês do ano passado, recuou 2,2%, acumulando queda de 1,8% no ano. Já no acumulado dos últimos 12 meses recuou 2,4%, a 33ª queda consecutiva.” Note que, apesar da manchete parecer positiva (mesmo sendo uma porcentagem praticamente desprezível), o índice vem acumulando diversas quedas consecutivas, revelando ainda um comportamento de recessão econômica nesse setor.

Falsas correlações

“33% dos acidentes de trânsito envolvem pessoas embriagadas. Portanto 67% das pessoas envolvidas em acidentes estão sóbrias. Logo, devemos dirigir bêbados que é mais seguro.”

A correlação é uma tentativa de explicar um fenômeno, cuja causa é desconhecida, baseado em outro fenômeno conhecido. Por exemplo, uma vez fizeram por brincadeira uma pesquisa de relacionar o número de nascimentos com o número de cegonhas em função do tempo. Notou-se que acontece um aumento do número de cegonhas na região ao mesmo tempo em que acontecem mais nascimentos. Conclusão (falsa): as cegonhas são responsáveis por trazer os bebês!

Perceba que nem sempre um fato está ligado ao outro. Dizer que um buraco que aparece na rua que nunca é fechado é culpa do presidente não é uma verdade só porque ele está no poder: buracos na rua são responsabilidade do poder municipal, e se não forem relatados pela população aos órgãos competentes, talvez nunca sejam descobertos pelos responsáveis por executar o serviço de manutenção.

As discussões sobre aquecimento global causam muita polêmica envolvendo estatística. Por exemplo, é comentado que a Terra vive ciclos de aquecimento e resfriamento, mas os críticos não consideram que a velocidade de aquecimento no último século foi mais acentuado do que ocorreria naturalmente, sem a ação do homem. A respeito de falsa correlação, em um determinado ano houve nevasca em certa região dos EUA. A primeira vista, pode parecer que estamos vivendo um resfriamento global, mas estatística não se faz com um ano só. Ao contrário, analisando-se as últimas décadas, nota-se que o normal era nevar na região, mas que fazia tantos anos que não nevava que as novas gerações não conheciam mais o fenômeno na região.

Outro exemplo de falsa correlação: no tempo da ditadura havia menos crimes e melhor educação, logo a ditadura é boa. Uma coisa não implica necessariamente em outra. E também como quantificar o “boa”? “Bom” e “ruim” são critérios subjetivos, e aí fica difícil comparar. Veja mais exemplos na matéria 10 mitos sobre a ditadura no Brasil.

“Comprovado: Fazer aniversário faz bem a saúde! Estatísticas mostram que pessoas que fazem mais aniversários vivem mais.”

Outro “causo” curioso: um senhor parado em um drive thru percebia que toda vez que ele pedia sorvete de pistache, o carro dele morria. Será que sorvetes de pistache fazem mal para o carro? O automóvel dele possui sistema de desligar depois de um determinado tempo parado. Então ele descobriu que o sorvete de pistache estava em um lugar mais distante da cozinha, e por isso ele esperava um tempo maior parado, causando o desligamento do motor.

Quando dois eventos distintos que não possuem qualquer relação entre si, mas que por uma questão do acaso, mostram intima relação estatística, isso é chamado “correlação espúria”. Veja mais exemplos no site Spurious Correlations.

O que os números dizem

“A morte de uma pessoa é uma tragédia; a de milhões, uma estatística.”
Frase erroneamente atribuída a Joseph Stalin

Milhões de pessoas morrem assassinadas, de fome e outras tragédias todos os anos que poderiam ser evitadas. Mas geralmente as pessoas só se preocupam quando a morte atinge alguma pessoa querida e/ou próxima.

Outro comentário também diz respeito à velocidade em que ocorrem as mortes. Se morrerem 6 milhões de pessoas em 3 anos devido a perseguições políticas e religiosas, isso pode ser considerado um genocídio. No entanto, se um valor próximo de pessoas morrer pelas mesmas razões em um período de 50 anos, isso não seria tão noticiado. É o caso do sapo em água quente: a água vai aumentando de temperatura gradualmente sem que ele perceba, até ficar cozido.

Muitas pessoas valorizam os parlamentares que nunca faltaram a uma sessão e alunos que sempre estão presentes nas aulas. Não que isso não seja motivo de parabenização, mas qual foi a produtividade deles? Existem parlamentares que veem filme pornô durante as sessões, assim como alunos que dormem ou conversam a aula toda.

Muitas vezes, os números que retratam a realidade brasileira são fruto de meras estimativas, como o número de abortos (atividade ilegal, difícil de contabilizar) ou o de famintos (questão que beira o subjetivismo).

Alteração dos critérios de contagem

Mudar a metodologia usada para calcular o número de homicídios pode reduzir os números referentes à criminalidade sem realmente as mortes terem diminuído. Talvez você lembre daquela frase do filme Tropa de Elite, “morte na praia é afogamento”, mesmo com várias perfurações de tiro no corpo. Veja mais algumas táticas:

• Calcular chacinas e casos com mais de uma vítima como sendo apenas uma ocorrência, independente do número de vítimas – afinal, a explosão de uma bomba atômica poderia ser considerado como apenas um caso de violência (Gestão Alckmin calcula taxa de homicídios fora do padrão mundial; essa matéria mostra um gráfico de como seria a taxa de homicídio considerando diferentes critérios);
• Não incluir casos de latrocínios (roubo seguido de morte) como homicídio (Alckmin altera divulgação para exaltar queda de crime);
• Excluir das estatísticas de homicídios dolosos as mortes cometidas por PMs de folga em legítima defesa (Assassinatos causados por PMs somem de estatísticas da gestão Alckmin)

Outros pontos que devem ser levados em consideração ao interpretar as estatísticas, como a magnitude da queda (1 morte a menos, por exemplo, não deixa de ser uma queda) e os valores absolutos (passar de 321 para 262 pessoas assassinadas por ano pode ser uma redução, mas ainda é muita gente).

Correção pela inflação

A inflação ocorre quando existe um aumento no suprimento de dinheiro e a expansão monetária, causando do aumento de preços pela lei de oferta e procura. Seu cálculo é feito através de um conjunto de produtos consumidos pela população em geral. No Brasil, existe o IPCA (Índice de Preços ao Consumidor Amplo) do IBGE, que apura a variação de preços nos bens consumidos por famílias com renda de 1 a 40 salários mínimos na principais regiões metropolitanas do país.

Dentre os itens utilizados para calular a inflação, está o de transportes. Um aumento na tarifa de ônibus nas regiões utilizadas para o cáclulo do IPCA impacta na inflação medida no país todo.

A comparação de valores antigos com atuais deve considerar a inflação. Por exemplo, é muito comum comparar a bilheteria de um filme recém lançado como sendo a maior da história. Porém, o preço do ingresso de cinema aumentou ao longo dos anos devido à inflação. Uma forma de corrigir isso é atualizar o valor médio do ingresso pago na época do lançamento para valores atuais e, aí sim, multiplicar pelo número de ingressos vendidos. O site do Banco Central tem uma calculadora que permite corrigir valores pela inflação.

A inflação deu a impressão de que os números de bilheteria do filme “Star Wars – O Despertar da Força” foram recordes, mas o faturamento real não superou o do filme original da saga, publicado em 1977 – mais detalhes na matéria da revista Galileu. O faturamento geralmente é utilizado como forma de medir o impacto do filme na sociedade, mas o número absoluto acaba falhando nesse quesito se considerar que antigamente existiam menos salas de cinema em menos países e uma população menor e em menos países, mas menor concorrência com outros filmes, dentre outros fatores.

Comportamento médio, e não um valor absoluto

“O estatístico é um sujeito que pode morrer afogado ao cruzar um rio com profundidade média de apenas 50 cm.”
W. I. E. Gates

Um número resultante de cálculos estatísticos geralmente não é um valor absoluto e verdadeiro, e sim um comportamento médio esperado. Esse intervalo numérico costuma aparecer em pesquisas eleitorais como margem de erro (“tantos pontos percentuais para mais ou para menos”). Não é possível afirmar “Fulano está vencendo as eleições” se estiver dois pontos percentuais acima do segundo candidato, já que existe uma margem de erro.

Ainda falando de pesquisas de intenção de voto, existem vários fatores que podem influenciar os resultados – por exemplo, fazer as pesquisas em redutos eleitorais de um mesmo candidato. Para quem não sabe, as pequisas são realizadas com um número pequeno de pessoas (por volta de mil a duas mil pessoas), nunca para toda a população. Daí a importância para considerar a margem de erro. Veja mais sobre como são realizadas as pesquisas de intenção de voto na matéria “Os números das estatísticas não mentem jamais. Será?“

Outro exemplo são as estatísticas de acidentes e mortes nas rodovias. Primeiro ponto, deve-se observar que todos os anos acontece um aumento no número de veículos, o que impacta na estatística: mais carros, maior a probabilidade de acontecerem acidentes.

Ainda com relação aos acidentes, todo feriado é publicado um balanço dessas variáveis, comparadas aos números do ano passado. Na Rodovia Régis Bittencourt, foi noticiada uma queda de 34% no número de mortes em 2015 no feriado de Carnaval comparado com 2014. Por regra de três, em 2014 morreram 9 pessoas em 2014. São números próximos de 1, portanto qualquer alteração já causa um grande impacto percentual – por exemplo, se em um ano morreu uma pessoa e no ano seguinte morreram 2, é matematicamente correto afirmar que houve um aumento de 100% no número de mortes, mas esse “100%” sugere algo muito mais impactante do que realmente é.

Existem estatísticas que são muito variáveis de um ano para outro. Por exemplo, veja esse gráfico do número de mortes em acidentes de moto na cidade de São Paulo:

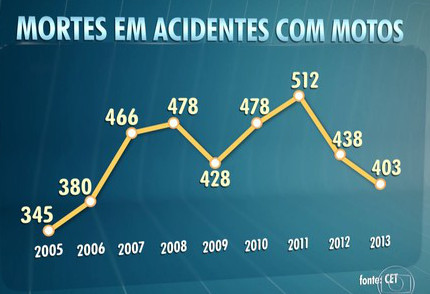
De 2008 para 2009, houve uma queda no número de mortos, mas se comparar com toda a série histórica, os valores flutuam em torno de uma valor médio, sem tendência considerável de aumento ou queda.

Em 2012 e 2013 aconteceram duas quedas sucessivas, mas para voltar aos valores de alguns anos atrás. Considerando que o número de motos e veículos tenha aumentado, pode ser considerada uma vitória, mas podem ser também pontos mais baixos na curva para nos anos seguintes voltarem a subir, já que os números variam bastante de um ano para outro: variabilidade grande, difícil explicação e difícil previsão.

Outras observações: se você dividir o número de mortes pelos dias do ano, é comum afirmar que morre pelo menos uma pessoa por dia de moto em São Paulo, mas não que todo dia deva morrer um – que nem o Quico (do programa “Chaves”) achava, já que a cada 20 minutos uma pessoa morria atropelada, podiam sair para brincar por 19 minutos até esperar o próximo ser atropelado e voltavam. É um valor médio.

Pelo gráfico, note também como é mais seguro viajar de avião do que de moto, já que em 2013 houve 72 mortes devido a acidentes aéreos em todo o país, segundo o Centro de Investigação e Prevenção de Acidentes Aeronáuticos (CENIPA).

Veja quanta informação um gráfico pode fornecer e mitigar problemas de interpretação. É comum observar notícias do tipo “bolsa sobe pelo terceiro dia seguido”. Quem escreveu essa notícia provavelmente quis passar uma ideia de recuperação econômica e que o cenário está favorável. No entanto, se observar um gráfico da série temporal de um ou dois meses, nota-se que o volume de negócios na bolsa caiu aos poucos de um nível médio para outro patamar, bem abaixo do normal. Assim, uma subida de três dias seguidos é o esperado.

Veja outro exemplo de notícia, agora a respeito de velocidade média de ônibus em São Paulo, que envolve vias exclusivas de tráfego e as vias não exclusivas. O texto considera a média como um valor absoluto, que apesar de ter uma grande variabilidade de valores que compõem esse item, essa variabilidade não é considerada para a análise:

“A queda foi tanto no horário de pico da manhã quanto no da tarde. No primeiro, das 7 às 10 horas, a queda foi de 17 km/h, em 2013, para 16 km/h no ano passado. À tarde, das 17 às 20 horas, a velocidade voltou de 16 km/h para 15 km/h.”

Considerando a velocidade média de vários ônibus em diferentes momentos como uma média contendo valores bastantes dispersos, pode-se até considerar que esses valores são estatisticamente iguais.

Certas vezes, é mais interessante trabalhar com outra grandeza estatística. A mediana é o valor do meio de um conjunto de dados (ou a média dos valores do meio, se o número de amostras for par). Por exemplo: a média de salários pode ser puxada para cima com um valor muito maior que os outros, fazendo parecer que todo mundo ganhe mais; isso vale também ao se considerar a renda per capita de um país com grande concentração de renda. Se o valor da mediana nesse caso for de mil reais, pode-se dizer que metade das pessoas ganha mais de mil reais e metade ganha menos.

Note também que a média não representa a maioria dos valores. Ainda no caso de países com grande concentração de renda, a grande maioria das pessoas vai receber abaixo de média, enquanto poucas vão receber acima da média e menos pessoas ainda vão receber perto do valor médio.

Cuidado com os gráficos

Os gráficos podem trazer muita informação de uma forma bem compacta e visualmente direta. No entanto, não estão livres de manipulações (intencionais ou isentas) que possam induzir conclusões erradas. Veja esse caso:

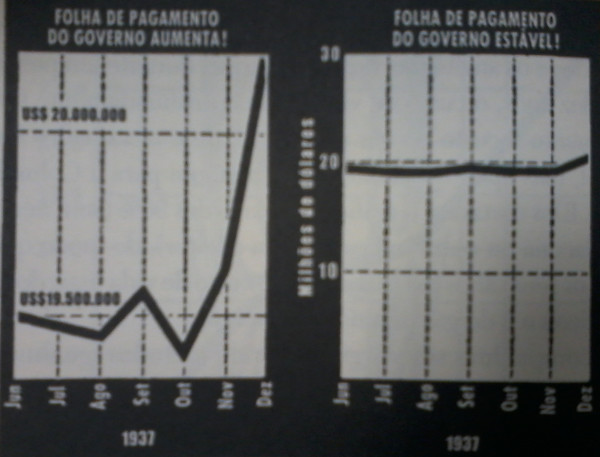
Uma simples mudança na escala pode mostrar que um aparente “vertiginoso crescimento” na verdade não representa uma porcentagem muito grande na variação de seu volume. Por outro lado, se uma variação pequena representar algo significativo, pode-se optar por “cortar” a escala (como feito no gráfico à esquerda), mas somente para efeito de visualização.

Uma série de gráficos tendenciosos, ou simplesmente mal feitos, pode ser vista no site WTF Visualizations.

Estatísticas futebolísticas

Comentaristas de futebol são extremamente subjetivos e emocionais. Afinal, como quantificar se um jogador (ou um time) é (ou está) melhor que outro? Existem diversas estatísticas de gols marcados, passes errados, chutes a gol, passes certos, dentre outras, que nunca são apresentadas durante as discussões. Por outro lado, é comum ouvir “tal time dispara na liderança” ou “o time está com 100% de aproveitamento”. São estatísticas válidas mas desprovidas de utilidade quando se está na primeira, segunda ou até mesmo quinta rodada de um campeonato com 38 rodadas! O então líder invicto do campeonato praticamente tem as mesmas chances de ser rebaixado que o último colocado a essa altura do campeonato.

Parece algo, mas não é

“Se você quer inspirar confiança, forneça muitas estatísticas. Não importa se elas estão certas, ou mesmo façam sentido, contanto que sejam muitas.”
Lewis Carroll

O número de área desmatada em um ano no Brasil geralmente equivale a centenas de estádios de futebol. No entanto quando esse número diminui de 1500 para 1100 “estádio” desmatados, o governo solta uma propaganda dizendo que o ritmo do desflorestamento está diminuindo. Isso sugere que estão parando de desmatar, mas não estão! E a taxa em si ainda é alta! E às vezes nem são realmente ações do governo que influenciaram na queda, e sim uma crise econômica que inibe o avanço do agronegócio sobre as regiões florestadas.

“Comprovado: Ovo de Páscoa não engorda! Cientistas pesaram diversos ovos em diferentes momentos e constataram que o peso continuou o mesmo.”

É muito comum utilizar estatísticas como argumento de autoridade para confirmar métodos e produtos que dizem fazer milagres, como emagrecimento rápido. Muitas vezes, certas medidas, cálculos e estudo são realizados sem o rigor do método científico – mesmo o famoso bordão “cientificamente comprovado” pode não estar atrelado aos procedimentos geralmente realizados pela Ciência. Por exemplo, testar medicamentos em um grupo muito pequeno de pessoas ou desconsiderar reações alérgicas ao produto tornam as estatísticas inválidas.

Existe uma probabilidade real de um cometa ou asteroide atingir a Terra, mas é de uma vez a cada 100 milhões ou 200 milhões de anos. Nosso planeta é bombardeado todos os dias por rochas de até um quilo, comuns no espaço, mas que se desintegram assim que entram na atmosfera. Então não é por que existe uma probabilidade de acontecer um evento que ele realmente vai acontecer – ou também que, por ser uma chance pequena de acontecer, que ele nunca ocorrerá.

Valor relativo e valor absoluto

“Um estatístico é um sujeito que se está com a cabeça num forno e os pés enterrados no gelo, ainda diz que na média a temperatura está ótima.”
K. Dunnigan

Existem muitos valores que são comparados a uma média histórica para saber se estão acima ou abaixo do comportamento esperado para aquele dia/mês/ano. Por exemplo: observa-se que o nível de um reservatório de água está 100% de sua média histórica durante os últimos 3 meses, mesmo em tempo de seca. No entanto, isso não quer dizer que o reservatório está com 100% de sua capacidade, e sim que ele está seguindo rigorosamente a média histórica. Se o preenchimento do reservatório de tantos milhões de litros (esse é o valor absoluto, que corresponde a 20% com relação ao seu volume total, por exemplo) para esse período do ano for baixo, ele está seguindo o comportamento da maioria dos anos para aquele mês.

Outro exemplo: em 16/04/2015, a SABESP (empresa que realiza os serviços públicos de saneamento básico no Estado de São Paulo) foi obrigada pela justiça a apresentar o nível do sistema Cantareira de abastecimento de água como negativo ao começar a utilização do chamado “volume morto”. Esse volume de água fica abaixo do nível de captação da represa somente pela ação da gravidade, sendo necessário realizar bombeamento para retirar a água do fundo da represa.

Na visão do Ministério Público, mostrar essa porção de água como positiva poderia induzir a população paulista de que o maior reservatório da Grande São Paulo está em condições melhores do que as reais. É como se você considerasse empréstimo para seu saldo ficar positivo (você tem dinheiro, mas não está positivo de verdade).

Ainda a respeito dos índices de volume das represas, uma comparação que pode ser enganosa é dizer simplesmente “o nível da represa subiu de ontem para hoje” quando aumentou 0,1 ponto percentual (de -9,2% para -9,1%, por exemplo). A impressão que se passa com essa afirmação é de que em poucos dias tudo voltará ao normal, o que não é verdade, já que a magnitude desse aumento é muito pequena perto do volume da represa. Esse valor não é um índice econômico, que a variabilidade dentro de minutos pode movimentar todo o mercado de ações, por exemplo. Deve ser analisado dentro de um período de vários dias ou mesmo meses, devido à lentidão de resposta do sistema ao seu preenchimento.

Limites tão altos que não há limites

Uma notícia sobre um acordo para a redução do açúcar na alimentação parece algo com que os produtores de açúcar devam se preocupar, mas analisando os números, é possível observar o “impacto”. O limite de açúcar em refrigerantes deverá ser de 11 gramas por 100 mililitros até o fim de 2020 e 10,6 gramas por 100 mililitros até o fim de 2022, mas um refrigerante da Coca-Cola, por exemplo, já tem 10,5 gramas de açúcar para cada 100 mililitros em 2018. Os achocolatados devem ter 90,3 gramas a cada 100 gramas até o fim de 2020 e 85 gramas por 100 gramas até o fim de 2022, mas em 2018 o Nescau já possui 75 gramas de açúcar para cada 100 gramas do produto.

“Olha, tesouro, eu poderia permitir que você comesse até 20 biscoitos. Mas por ter me enganado com a história da estrela, não vai comer mais que 18! Nem um a mais!”
Dona Florinda reprimindo Quico

Além do acordo impor restrições com valores mais altos do que os já em prática pela indústria de alimentos processados, é interessante avaliar o porcentual de açúcar na composição do alimentos. Um consumidor leigo espera que um achocolatado tenha o chocolate como maior parte de sua composição, mas nota-se que o açúcar é o componente principal, e que 90,3 gramas para cada 100 gramas é mais de 90% da composição em açúcar.

Em 2007, foi assinado um acordo que buscava a redução de sódio nos alimentos processados. A ABIA (Associação Brasileira das Indústrias da Alimentação) afirmou que fez a “retirada de mais de 17.254 toneladas de sódio de 35 categorias de alimentos industrializados”. Parece muita coisa né? Dividindo esse valor pela população brasileira em 2007 (190 milhões), chega-se a uma redução anual de oito gramas por pessoa, ou 0,022 grama por dia. Uma pesquisa do Instituto de Estudos em Saúde Coletiva da UFRJ (Universidade Federal do Rio de Janeiro), realizada em 2014, mostrava que quase metade dos produtos avaliados (49,5%) não seria afetada pelas metas definidas para 2017 – já estavam dentro da meta.

Preços

Outra forma de manipular as pessoas através de números são com os preços cobrados por produtos e serviços. A Black Friday é um grande exemplo. Esse termo foi criado pelo varejo nos Estados Unidos para nomear a ação de vendas anual com grandes descontos que acontece na sexta-feira após o feriado de Ação de Graças. Um dia antes, os preços recebem um grande aumento para que, no dia do evento, eles recebam um grande desconto. Essa tática é conhecida como “o dobro pela metade” do preço, já que pode-se aumentar o valor para que na Black Friday o preço volte ao valor original, mas o consumidor pensa que está comprando por um preço muito baixo. Ainda existem as promoções nas quais é colocado um valor como se fosse o preço antigo, muito mais alto que o preço cobrado no momento. Por exemplo: dia 24/11, o computador custava 1500 reais, e no dia seguinte aparece uma placa dizendo “de 1800 por 1500 reais”.

Existem outras práticas comuns, como colocar o valor de um produto como “999,00”, por exemplo, para dar a ideia de que o preço não chega à casa do milhar. Isso leva as pessoas a pensar que o produto custa “900 e pouco” e não que está praticamente custando mil reais. É comum ver em postos de gasolina preços cobrado em milésimos de real com o mesmo intuito. Por exemplo, 3,499 o litro da gasolina para dar a ilusão de que é 3,40 e pouco, enquanto que o valor está bem mais próximo de 3,50 – multiplicando o valor por vários litros, faz uma diferença no bolso e no caixa do dono do posto.

Um ponto importante na comparação dos preço de produtos vendidos por peso/volume/etc é preço por unidade de medida, já que as marcas são vendidas em embalagens com diferentes pesos. Por exemplo, uma embalagem com 1 litro de refrigerante custa 2 reais e o concorrente custa 3 reais, mas a embalagem tem 2 litros. Assim, a primeira marca está cobrando R$2,00/litro de refrigerante, enquanto que a segunda cobra R$1,50/litro. Para obter esse valor, basta fazer uma regra de três para obter esse valor (ou dividir o preço pela unidade). Por isso muitos supermercados colocam o preço por unidade na etiqueta de preço da gôndola – inclusive já existe projeto de lei para tornar isso obrigatório.

Também é comum apresentar o valor parcelado em destaque com o valor de venda a vista mais escondido, passando uma primeira impressão de que o valor da parcela seria o preço total. Além disso, existem aquelas promoções com “letras miúdas” escritas embaixo e que restringem a número de peças, período de compra (inclusive com horário), vendas casadas, etc. Essas práticas ocorrem também em diferentes épocas do ano e em vários estabelecimentos. Por isso é importante pesquisar o mesmo produto ou serviço em diferentes estabelecimentos comerciais e durante vários dias. Quanto maior o valor do produto, mais importante é a pesquisa de preços e calma para fazer a compra.

Como Não Ser Enganado com Estatística

O livro “Como Mentir com Estatística”, de Darrell Huff, propõe cinco perguntas para validar uma estatística apresentada para você:

1) Quem é que diz isso?

Procure sempre saber quem está divulgando a estatística. Por exemplo, o governo anuncia que o salário mínimo aumentou 3% no último ano. Quem vê o valor isoladamente, pensa que está ganhando mais. No entanto, se no mesmo período houve inflação de 7%, o poder de compra diminuiu muito mais do que o ganho no salário. Isso é chamado arrocho salarial.

As respostas em entrevistas e questionários podem ser influenciadas por fatores sociais (mais entrevistados de uma mesma classe social, por exemplo), local/ambiente, postura do entrevistador (afinidades, preferências…), ordem das questões e também alguns grupos tem suas informações mais bem coletadas que outros (nascimentos em metrópoles são melhor registradas do que no sertão, por exemplo).

Em um vídeo do GEMA (Grupo Escolar de Mídia Alternativa), foi feito um vídeo com uma entrevista em que se perguntava sobre cortar algumas árvores para construir um estacionamento. As perguntas feitas antes da pergunta principal induziam um determinado tipo de resposta final nos entrevistados. Por exemplo, fizeram perguntas sobre a importância de se cuidar do meio ambiente e depois perguntar do corte de árvores induzia os entrevistados a não tirar as árvores. Para outro grupo, primeiro perguntaram sobre se era difícil achar lugar para estacionar e depois fizeram a pergunta da remoção das árvores, obtendo um resultado favorável à exclusão delas.

O entrevistador acaba tendo um grande peso na resposta. O entrevistado se sente influenciado pela aparência do entrevistador. Por exemplo, quando são da mesma etnia em um ambiente de forte pressão social, as respostas tendem a ser mais sinceras. Ou também o entrevistador tem duas pessoas para escolher entrevistar na rua: uma pessoa limpa e outra suja, qual ele vai escolher?

2) Como é que ele sabe?

Descubra de onde vem a informação, como que ela foi gerada. Utilizando uma pequena amostra o resultado obtido pode ter ocorrido totalmente por acaso. Se alguém diz que, após tratar dez ratos diabéticos com certa erva medicinal, sua taxa de glicose baixou 2,4%, isso pode ser uma coincidência devido ao baixo número de amostras – se tivesse sido testada em 100 ratos, talvez somente 15 tivessem redução de glicose e em 85 não fizesse efeito algum, ou até aumentasse a taxa.

3) O que é que está faltando?

Há casos em que os número brutos são suprimidos e apenas os percentuais são apresentados, e em outros casos é justamente o contrário. Por exemplo: dizer que 33,3% dos alunos não foram aprovados no curso de inglês pode ser preocupante, mas se na sala de aula tinham só três alunos, significa que somente um aluno reprovou. Ou também um jornal afirmar que a safra de um ano é quatro vezes maior do que a do ano anterior, mas que nesse ano anterior teve uma grande seca que dizimou boa parte da safra prevista.

4) Alguém mudou de assunto?

Se alguém constata que o número de casos COMUNICADOS de uma doença aumentou e depois diz que o número de casos OCORRIDOS da doença aumentou, somente uma palavra já muda o assunto. Uma maior precisão nos diagnósticos que agora classificam como câncer de mama o que antes era “mal de peito” pode explicar essa “falsa epidemia” que teria aparecido. Ou também dizer que o número de tornados está aumentado, sendo que antigamente os tornados duram poucos minutos e aconteciam em regiões desabitadas e sem monitoramento meteorológico; o que acontece aqui na verdade é um aumento no número de registros de tornados, mas não significa necessariamente que o número de ocorrências aumentou.

5) Isso faz sentido?

Avaliar com bom senso se a estatística faz sentido com os fatos ao seu redor pode nos proteger de cair em muitas falácias. Usar tendências antigas, observadas em épocas em que o mundo era muito diferente do que é hoje é extremamente perigoso. Por exemplo, afirmar que o número de estupros é maior atualmente do que nos anos 1970 desconsidera o fato de que as mulheres sentiam-se muito mais constrangidas em denunciar seus agressores, ou seja, na verdade o número de casos COMUNICADOS é que aumentou.

“Comprovado: Fazer aniversário faz bem a saúde! Estatísticas mostram que pessoas que fazem mais aniversários vivem mais.”

Veja mais sobre como convencer as pessoas no post Retórica e comportamento humano e outros exemplos de estatísticas mal interpretadas no post sobre previsão de tempo.

Posts relacionados:

Teoria de Resposta ao Item Entrevista: matemático e artista Portfólio – Editora Testes de Hipóteses e de Aderência