As equações de Maxwell são um grupo de equações que, juntamente com a lei da força de Lorentz, compõe a base do eletromagnetismo clássico, e no qual está incluída toda a óptica clássica. Seu entendimento contribuiu significativamente para toda uma revolução tecnológica iniciada no final do século XIX e continuada durante as décadas seguintes. Veja um pouco mais sobre essas equações tão fundamentais para o entendimento da natureza e algumas aplicações como a polarização e o entendimento do azul do céu.
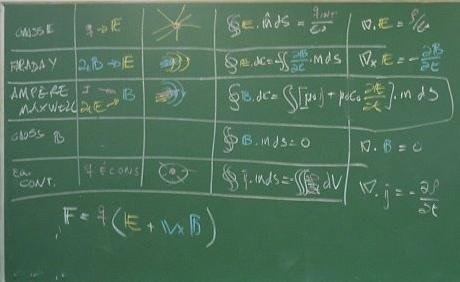
O Eletromagnetismo é a teoria unificada, desenvolvida por James Maxwell (1831-1879), para explicar a relação entre eletricidade e magnetismo. A partir do conhecimento existente na época, como a Lei de Coulomb, de Ampère, etc, Maxwell descobriu correlações entre alguns fenômenos e estabeleceu algumas leis básicas do Eletromagnetismo, conhecidas como Equações de Maxwell.
- Lei de Gauss (relaciona carga com a distribuição radial do campo elétrico)
\(\nabla.\vec D=\rho\)
- Lei de Faraday (relaciona a variação temporal do campo magnético com o campo elétrico)
\(\nabla\times\vec E=-\frac{\partial\vec B}{\partial t}\)
- Lei de Ampère-Maxwell (relaciona corrente elétrica e variação temporal do campo elétrico com campo magnético)
\(\nabla\times\vec H=\vec j+\frac{\partial\vec D}{\partial t}\)
- Lei de Gauss Magnética (Lei de Gauss aplicada ao caso do inexistente monopolo magnético):
\(\nabla.\vec B=0\)
onde (as unidades no SI estão entre parênteses):
\(\rho\) é a densidade de carga (C/m³);
\(\vec B\) é a densidade superficial de fluxo magnético, ou indução magnética (T);
\(\vec E\) é a intensidade de campo elétrico (C);
\(\vec D=\varepsilon\vec E+\vec P\) é a densidade superficial de campo elétrico, ou campo elétrico de deslocamento (C/m²), sendo \(\varepsilon\) a permissividade elétrica1 (ou constante dielétrica), e \(\vec P\) é a polarização (somatório dos momentos de dipolo2, que aparecem devido aos constituintes ou induzidos por um campo externo);
\(\vec H=\mu\vec B\) é a intensidade do campo magnético(A/m), e \(\mu\) é a permeabilidade magnética3.
Em termos físicos, o divergente de um vetor em um campo tridimensional pode ser entendido como um fluxo direcional comportando-se como uma fonte ou sorvedouro em um dado ponto. O rotacional pode ser descrito como a densidade de circulação. Note a semelhança do comportamento matemático no Eletromagnetismo com a Mecânica de Fluidos, pois se acreditava que a eletricidade fosse realmente um fluido, pensando-se o mesmo sobre o calor: um material capaz de penetrar os vazios da matéria e escoar.
As soluções das equações de Maxwell são as equações de onda que descrevem os campos elétrico e magnético no espaço-tempo. Assim, a luz é uma propagação de uma perturbação eletromagnética. As diferentes frequências de oscilação então associadas a diferentes tipos de radiação.
Devido à linearidade da equação de onda, qualquer onda pode ser decomposta em ondas planas monocromáticas, o que é chamado de princípio da superposição. Uma onda é monocromática quando oscila com uma única e bem definida frequência e é plana quando os campos elétrico e magnético forem, em cada instante, constantes ao longo de um plano perpendicular à direção de propagação (no caso, adotou-se a direção y). Assim, a solução é representada pelas equações:
\(\vec E=(E_{0x}\vec i+E_{0z}\vec k)cos(ky-\omega t+\phi)\)
\(\vec B=\frac{1}{c}\vec j\times\vec E\)
onde \(E_{0x}\) e \(E_{0z}\) descrevem a amplitude da onda nas direções x e z, \(\omega=2\pi/T\) , sendo T o período, \(k=2\pi/\lambda\) , sendo \(\lambda\) o comprimento de onda, e \(\phi\) uma fase fixada pelas condições iniciais. Note que os campos elétrico e magnético são perpendiculares entre si e também à direção de propagação. Uma variação do campo elétrico gera um campo magnético que, por ser variável, gera um campo elétrico induzido… gerando a perturbação eletromagnética que se propaga através do espaço. No vácuo, a velocidade de propagação é \(c=1/\sqrt{\varepsilon_0\mu_0}\).
Os campos elétrico e magnético arrastam consigo as densidades de energia através do espaço. Esse fluxo de energia é representado pelo vetor de Poynting1:
\(\vec S=\frac{\vec E \times\vec B}{\mu_0}\)
A intensidade do fluxo de energia é definido como o valor médio do módulo do vetor de Poynting da onda em um período:
\(I=\lt S\gt=\frac{1}{T}\int_0^T Sdt\)
No sistema internacional, a energia é dada em joules, sendo o fluxo da energia radiante dada em joules por segundo (Watt). A irradiância será a quantidade de energia radiante que incide sobre uma superfície horizontal ou área unitária por unidade de tempo (W/m²). Relembrando, o joule (J) é o trabalho produzido por uma força de 1 newton (N) cujo ponto de aplicação se desloca 1 metro na direção da força, e Newton é a força que transmite a aceleração de 1 m/s² a um corpo de massa 1 kg.
Polarização
A orientação das oscilações do vetor de campo elétrico, estudada no plano perpendicular à propagação da onda, é dada pela polarização. Por exemplo, uma onda é linearmente polarizada se a extremidade do vetor campo elétrico, num dado ponto do espaço, traça uma reta com o passar do tempo. Observe na figura a seguir diferentes estados de polarização.

A luz do Sol é incoerente, ou seja, possui várias frequências em diferentes direções e fora de fase, devido ao fato da emissão da luz ser espontânea (ocorre ao acaso). Para se obter luz polarizada, pode-se utilizar um polarizador, que permite a passagem de ondas com polarização ao longo de uma certa direção e bloqueia ondas com polarização diferente. O campo elétrico com polarização não alinhada com a do polarizador gera correntes no polarizador, sendo sua energia absorvida.
Uma das formas de polarização da luz é por espalhamento (“desvio da direção de propagação”). A luz do céu azul é bastante polarizada devido ao espalhamento da luz pelos gases da atmosfera. Devido à ressonância das moléculas constituintes da atmosfera com o azul, a eficiência de espalhamento do azul é maior. Quando ocorre o pôr ou nascer do Sol, o caminho que a luz percorre é maior. A componente azul da luz solar é espalhada para regiões da Terra onde ainda é dia, restando apenas as componentes com frequência menor como o vermelho. Esse efeito é acentuado quando ocorre mais espalhamento devido a partículas suspensas no ar, como em fins de tarde poluídos. Também devido à ressonância, agora na região do infravermelho, a água e o gás carbônico absorvem e reemitem radiação infravermelha emitida pela Terra e causam o efeito estufa.

Veja mais sobre polarização do céu clicando nesse link e sobre o pôr do sol no respectivo item desse post.
Veja também sobre o que são: radiação e onda eletromagnética e Onda eletromagnética em meio material nesses links.
Notas
1 Permissividade elétrica: descreve como um campo elétrico afeta e é afeto por um meio dielétrico (isolante, possui alta resistência à condução de corrente elétrica), e determina a habilidade do material em polarizar-se como resposta a um campo externo.
2 Dipolo elétrico: separação de cargas positiva e negativa, caracterizado pelo vetor momento de dipolo, que aponta da carga negativa para a positiva com a magnitude dada pelo produto da intensidade das cargas pela distância de separação.
3 Permeabilidade magnética: grau de magnetização de um material em resposta a um campo magnético.
4 John Henry Poynting (1852-1914): físico inglês.
Bibliografia
- BECHARA, M. J., DUARTE, J. L. M., ROBILOTTA, M. R., VASCONCELOS, S. S., Física 4 – notas de aula, São Paulo, 2002.
- Forrest Mims, Texas Observatory – http://www.polarization.com/sky/Forrest_Mims_Polarized_sky_sunset_0804201_Dscn5167.jpg, acessado em 21/06/08.
- Polarization singularities in the clear sky – http://www.iop.org/EJ/article/1367-2630/6/1/162/njp4_1_162.html – acessado em 21/06/08.
- HZN, J. J. Vos, COEMANS, M. A. J. M. & NUBOER, J. F. W., No evidence for polarization sensitivity in the pigeon electroretinogram, The Journal of Experimental Biology, 1995. http://jeb.biologists.org/cgi/reprint/198/2/325.pdf
- NUSSENZVEIG, H. M., Curso de Física básica, volume 2, São Paulo, Ed. Edgard Blücher, 1981.





2 comments