Na geometria euclidiana, as figuras geométricas usuais têm dimensões representadas por números inteiros: 0 – ponto, 1 – linha, 2 – superfície, 3 – volume. No entanto, se o litoral de um país for medido com uma régua de 1 metro ou de 1 centímetro, serão obtidas diferentes medidas. Assim, existem objetos cuja dimensão não pode ser representada por números inteiros, mas números fracionários, chamada de dimensão fractal.
O matemático francês de origem judaico-polonesa Benoît Mandelbrot (1924-2010) tentou medir o comprimento da costa da Grã-Bretanha (Mandelbrot, 1967). Ele descobriu que o comprimento medido depende da escala de medição: quanto menor o incremento de medição, maior o comprimento medido. Assim, as formas fractais não podem ser medidas com um único comprimento característico, devido ao padrão repetido que descobrimos continuamente em diferentes níveis de escala. Esse crescimento do comprimento segue uma lei de energia encontrada empiricamente por Richardson (Richardson, 1961) e citada por Benoit Mandelbrot em seu artigo de 1967:
\(L(n) \propto n^{-a}\)
onde L é o comprimento da costa, n é o comprimento da medida utilizada e o expoente a representa a dimensão fractal da costa.
Outra propriedade principal dos fractais é a auto-similaridade, ou seja, um objeto é composto de subunidades e subunidades, em vários níveis, que lembram a estrutura de todo o objeto. Portanto, as formas fractais não mudam, mesmo quando observadas em diferentes escalas, o que é chamado de invariância de escala. No entanto, no mundo real, essa auto-similaridade é observada apenas em algumas escalas.
Muitos processos descritos por séries temporais podem ser considerados fractais em suas descrições gráficas. A dimensão fractal permite quantificar a variabilidade de uma série temporal. Como método preciso para estimativa da dimensão fractal dos sinais temporais discretos, Harrouni (2008) desenvolveu um método simples baseado em uma cobertura por retângulos chamada Método de Cobertura Retangular (“Rectangular Covering Method”), baseado na abordagem Minkowski–Bouligand.

Nesse método, a curva da série temporal de irradiância é coberta por retângulos de mesma diferença temporal, cujos vértices opostos são os pontos em t e t+\(\Delta t\). O somatório da área desses triângulos é dado por:
\(S(\Delta\tau,\Delta t)=\sum\limits_{t=0}^{N-1}|f(t_n+\Delta \tau)-f(t_n)|\Delta \tau\)
onde N é o número total de amostras do sinal, \(f(t_n)\) é o valor do sinal no instante \(t_n\) e o valor absoluto relaciona-se ao intervalo de tempo \(\Delta\tau\). Quanto menor for esse intervalo, maior o comprimento medido.
A dimensão fractal D representa o ângulo de inclinação da reta ajustada conforme a seguinte equação, calculada para diferentes valores de \(\Delta\tau\):
\(ln\left ( \frac{S(\Delta\tau, \Delta t)}{\Delta\tau^2} \right )= D(\Delta t) ln \left ( \frac{1}{\Delta\tau} \right ) + C\)
Deve-se escolher um \(\Delta\tau\) inicial, sem exceder N/2, e outros cada vez menores de 1 em 1. Utiliza-se o método de mínimos quadrados em um gráfico log-log para calcular o coeficiente angular da reta ajustada. À medida que aumentamos a frequência de medição, a dimensão fractal converge para um, que é a dimensão correta para uma linha.
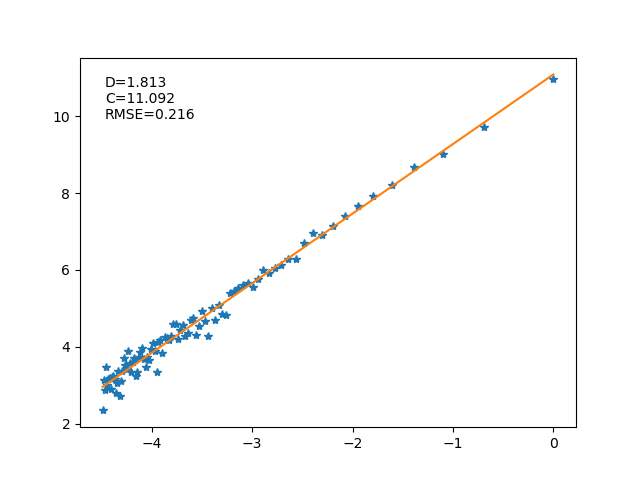
Foi feito um script em python que lê os dados em um arquivo CSV e executa o algoritmo descrito para o cálculo da dimensão de uma série temporal. Os dados foram retirados de valores de irradiância global medidos por um piranômetro da rede sonda/INPE e estão disponíveis juntamente com o código no Github (viniroger/fractal).
Os dados são carregados para um dataframe e a série temporal é plotada em um gráfico (função “plot_data”). Os cálculos dos somatórios das áreas dos retângulos são realizados na função “calc_Sdtau”, onde é criado um loop para os diferentes valores de intervalos (\(\Delta\tau\)). Para cada tamanho de intervalo, é percorrida toda a série, onde um ponto e o seguinte são vértices opostos do retângulo cuja área deve ser calculada.
No final dos loops, a função “calc_dim” faz o somatório das áreas relacionadas a cada \(\Delta\tau\), gerando um ponto para cada um desses intervalos. Por fim, calcula-se um ajuste de reta, onde o coeficiente angular é a dimensão fractal da série temporal.
Fontes
- Blaga, Robert & Paulescu, Marius. (2018). Quantifiers for the solar irradiance variability: A new perspective. Solar Energy. 174. 606-616. 10.1016/j.solener.2018.09.034.
- Harrouni, S., 2008. Fractal classification of typical meteorological days from global solar irradiance: Application to five sites of different climates. In: Badescu, V. (Ed.), Modeling Solar Radiation at the Earth Surface. Springer, Berlin, pp. 29–54.
- Mandelbrot B (1967) How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science, New Series 156:636–638
- Richardson LF (1961) The problem of contiguity: an appendix of statistics of deadly quarrels. Genmal Systems Yearbook 6:139–187