A distribuição normal descreve uma série de fenômenos físicos e financeiros, possuindo grande uso na estatística. Ela serve de aproximação para o cálculo de outras distribuições, conforme o Teorema central do limite: quando o tamanho da amostra aumenta, a distribuição amostral da sua média aproxima-se cada vez mais de uma distribuição normal. Quando plotada em um gráfico, tem forma de sino.
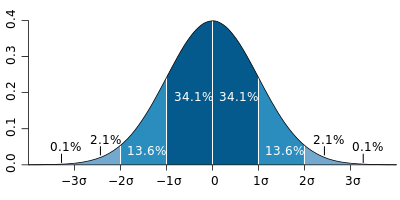
Gráfico de distribuição normal normalizada, representadas as áreas com um (68% da área), dois (95%) e três (99,7%) desvios padrões. Fonte: Wikipedia
Conhecendo-se seus parâmetros de média μ e desvio padrão σ, consegue-se determinar qualquer probabilidade. A função densidade de probabilidade da distribuição normal é assim definida:
É comum essa função ser representada usando média igual a zero e desvio padrão igual a um. Se a variável aleatória x segue esta distribuição, escreve-se que x ~ N(μ,σ2).
Note pelo gráfico que a área sob a curva representa a probabilidade. No entanto, existem diferentes formas (ou seja, diferentes valores de z) para se obter uma mesma área. Veja esse exemplo para probabilidade igual a 95%:
O valor de z que tem 95% dos dados abaixo dele ignorando apenas a cauda superior (unilateral) é 1,645 enquanto que ignorando ambas as caudas (bilateral), esse valor passa para 1,96.
Existem programas (como a função “norm.ppf” do pacote “scipy.stats” do Python), que considera como padrão ignorar apenas a cauda superior. Considerando-se que a distribuição normal é simétrica, pode-se dividir a quantidade que ignorada ao meio para obter apenas a cauda superior ignorada (no caso, 0,5/2 = 0,25). Nesse caso, temos que considerar p = 0,975 para obter z = 1,96.
É comum utilizar tabelas para consultar a relação entre o valor da área (probabilidade) e o valor de z. O vídeo a seguir também mostra como usar a tabela da distribuição normal:
Uma calculadora online de probabilidades da distribuição normal (com gráfico) disponível no link realiza a conversão facilmente, permitindo considerar diferentes intervalos e valores de desvio padrão, média e área.
Fontes
- Wikipedia – Distribuição Normal
- Stackoverflow – Probability to z-score and vice versa in python

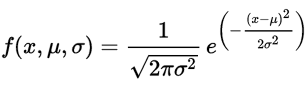





3 comments