Teoria dos erros

Ao se fazer qualquer medição (de tempo, massa, velocidade, etc), o valor obtido está sujeito a erros e incerteza, que podem ser grandes ou pequenos. Por exemplo, no dia a dia não faz muito sentido a precisão de segundos para marcar um encontro, mas se em uma fábrica de tecidos existe uma diferença de alguns centímetros no corte de um tecido, isso pode gerar muitos prejuízos. Veja mais sobre esses e outros conceitos (como média e desvio padrão) para fazer medições de boa qualidade em medições sucessivas e sob as mesmas condições.

“Quando você pode medir o que você está falando, e expressá-lo em números, você conhece alguma coisa sobre ele; quando você não pode expressá-lo em números o seu conhecimento é imperfeito.”

Lord Kelvin, Cientista britânico (1824 – 1907)

“Erro” é a diferença entre um valor medido e um valor verdadeiro de uma grandeza. “Incerteza” é a quantificação da dúvida sobre o resultado da medição. Sob uma outra óptica, uma grande diferença entre esses dois conceitos é que o erro pode, em princípio, ser “corrigido” enquanto a incerteza é um intervalo da confiança dessas medidas.

O “valor verdadeiro” seria conhecido apenas sob condições ideais, sem fontes de erros atuando. Na prática, esse valor é obtido a partir de uma medida de referência, na qual é utilizado o conhecimento científico mais avançado possível sobre os processos envolvidos.

O grau de concordância entre um valor medido e um valor verdadeiro é conhecido como “exatidão” (ou acurácia). Difere do conceito de “precisão“, que é a proximidade entre resultados de diversas medições independentes (utilizando-se os mesmos métodos e condições) de uma mesma variável. Sempre haverá uma incerteza na medição, mesmo quando as medições são precisas e exatas.

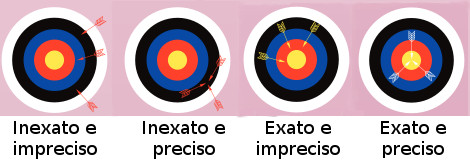
Tipos de erros

Erro sistemático (ou tendenciosidade) – erro que afeta igualmente todas as medições (valores aparecem deslocados com relação ao valor verdadeiro). Pode ser de origem instrumental, ambiental ou observacional (por exemplo, realizar a leitura de um termômetro sempre olhando de um ângulo errado, em vez de observar diretamente). É quantificado pela grandeza chamada viés.

Erro aleatório (ou estatístico) – resulta de variações aleatórias nas medições, provenientes de fatores que não podem ser (ou não foram) controlados. Por exemplo, correntes de ar ou vibrações podem introduzir erros estatísticos na medição da massa de um objeto com a balança.

Erros grosseiro (ou espúrios) – falhas humanas esporádicas ou mau funcionamento do instrumento.

Existem algumas grandezas estatísticas que permitem avaliar a relação entre os valores observados e os previstos teoricamente:

Erro médio – Média das diferenças entre valor o previsto e o observado. Quanto maior a diferença, pior a previsão (ou pior a medida observada). Como se trata de uma diferença (subtração), caso o sinal seja positivo, o valor previsto é menor que o observado (em média), o que indica uma tendência do modelo teórico subestimar. Caso o sinal seja negativo, tendência do modelo superestimar. O melhor é ter um erro próximo de zero. No entanto, se metade das diferenças forem positivas e outra metade negativa com a mesma magnitude, o erro também será zero. Precisa analisar o erro médio absoluto para interpretar melhor.

Erro médio absoluto – Média das diferenças absolutas (ou seja, em módulo) entre valor o previsto e o observado. Quanto maior a diferença, pior a previsão (ou pior a medida observada). Como o valor somado na média está em módulo, é possível avaliar melhor a magnitude do erro, em vez de suas tendências em subestimar ou superestimar – quanto mais próximo de zero, melhor a previsão do modelo.

Incerteza

A incerteza é definida como um “parâmetro associado ao resultado de uma medição e que caracteriza a dispersão dos valores que podem ser fundamentalmente atribuídos ao mensurando”. Em outras palavras, é uma quantificação da dúvida que existe em relação a um resultado de qualquer medição.

A incerteza é requerida para decidirmos se o resultado é adequado para seu propósito e consistente com outros resultados similares. Sempre acompanha a medida, independente da exatidão do instrumento. Por exemplo, ao medirmos um objeto com 200 cm com um nível de confiança de 95%, temos que deverá ser expressado da seguinte forma: 200 + 1 cm (ou seja, temos 95% de certeza que o comprimento do objeto está entre 199 cm e 201 cm). Caso o valor não seja informado pelo fabricante do instrumento, utiliza-se a metade da menor divisão da escala (no caso de uma régua simples, seria 0,5 cm). Por exemplo, uma balança que meça em quilos registraria o valor de 70,1 + 0,5 kg (dessa forma, se acha que emagreceu 200 gramas, na verdade isso pode estar dentro da incerteza da balança).

Média e desvio padrão

Ao falarmos de incerteza, note que falamos sobre a probabilidade da medição pertencer a um intervalo de valores. O valor médio seria o valor mais provável (que seria obtido com um número infinito de medições), calculado através da soma dos valores amostrados e dividindo-se o resultado pelo número de amostras – esse cálculo é chamado de média aritmética.

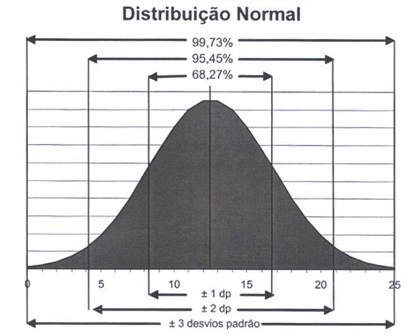
Uma quantificação da dispersão dos resultados obtidos por uma série de medições é chamada desvio padrão, sendo representado pela seguinte fórmula (geralmente identificada pela letra “s” ou pela letra grega sigma):

\(\sigma=\frac{\Sigma(X_i-X_m)}{n-1}\)

Essa fórmula representa o somatório das diferenças entre os x_i valores e a média (x_m), dividido pelo número de amostras menos um. Caso esse valor obtido seja dividido pela raiz do número de amostras, será obtido o valor do desvio padrão da média.

Veja uma aplicação do conceito de desvio padrão: duas salas de aula com média de idade 25,4 e 28,5 podem ser considerados como um mesmo grupo? A princípio não: médias diferentes, grupos diferentes. No entanto, deve-se considerar o desvio padrão para observar se os valores de média são compatíveis entre si. Um aluno mais velho pode “puxar a média” da sala para cima, o que é revelado por um desvio padrão maior desse grupo.

O desvio padrão é simplesmente o resultado positivo da raiz quadrada da variância. O denominador “n–1” da variância é determinado graus de liberdade. Grau de liberdade é número de determinações independentes (dimensão da amostra) menos o número de parâmetros estatísticos a serem avaliados na população, ou também o número de escolhas livres/independentes depois que uma estatística (como a média) é calculada. No caso especifico do cálculo da variância, diz-se que os n graus de liberdade originalmente disponíveis no conjunto sofreram a redução de uma unidade porque uma estatística, a média já foi calculada dos dados do grupo e aplicada na determinação da variância. Também pode ser determinado pelo número de caselas em uma tabela que teriam preenchimento livre considerando que temos as totalizações de linhas e colunas: (l-1).(c-1), sendo l o número de linhas e c o número de colunas.

Existem outras grandezas estatísticas importantes cujas definições estão baseadas na média e no desvio padrão – veja mais no post sobre Estatística.

Distribuição t de Student

Existem outras curvas de distribuição de probabilidades, como a t de Student. Desenvolvida por Willian S. Gosset em 1908, publicou suas descobertas sob o pseudônimo Student enquanto trabalhava nas cervejarias Guinness (Irlanda) visando resolver problemas relacionados às pequenas amostragens, que não se comportavam como previsto pela distribuição normal. A distribuição t é semelhante à normal, porém com caudas mais largas. Quanto mais graus de liberdade, mais próxima da normal será a curva.

Referências

• Propagação de erros e incertezas
• INMETRO – Rastreabilidade e incerteza
• Introdução à Teoria de Erros