Em um modelo de Redes Neurais Artificiais (RNA), a seleção de entradas (dados) e a estrutura (número de neurônios e como estão conectados) são pontos geralmente definidos iterativamente ou ad hoc. No entanto, os critérios de projeto podem incluir múltiplos objetivos conflitantes, o que confere ao problema de identificação do modelo um caráter de otimização combinatória multiobjetivo. Algoritmos evolutivos de otimização multiobjetivo são particularmente adequados para resolver esse problema porque podem desenvolver estruturas de modelos otimizados que atendam a critérios de projeto pré-especificados em um tempo de computação aceitável.
A maioria das aplicações práticas de RNA tem como objetivo realizar um mapeamento não linear entre um espaço de entrada e um espaço de saída, a fim de modelar relações complexas entre estes ou para detectar padrões em dados de entrada-saída. Estas funcionalidades correspondem principalmente a problemas de aproximação de funções no contexto de identificação de modelos estáticos ou dinâmicos, ou a problemas de decisão em contextos de correspondência e classificação de padrões.
Considerando a aplicação em questão, deve-se selecionar um certo número de recursos (características, ou “features” em inglês) e um número adequado de neurônios para definir o vetor de parâmetros da RNA, de modo a obter o melhor mapeamento da RNA. Para isso, uma ou mais medidas de qualidade são necessárias para que quaisquer duas soluções diferentes de RNA possam ser comparadas e uma decisão possa ser tomada sobre qual é a melhor.
O problema de busca do melhor mapeamento é um problema de otimização combinatória multiobjetivo que não possui uma solução única minimizando todos os componentes simultaneamente. Em vez disso, a solução é o conjunto de pontos de Pareto que definem a frente de Pareto no espaço de objetivos.
A Fronteira/Frente de Pareto é um conceito da economia e teoria de jogos desenvolvido pelo economista italiano Vilfredo Pareto (não é o Luiz Pareto :P). Essa teoria descreve um estado no qual é impossível melhorar uma situação para uma pessoa sem piorar a situação de outra. Na prática, essa fronteira é usada para ilustrar situações onde se busca maximizar um conjunto de resultados, considerando que as melhorias em um aspecto podem resultar na piora de outro. Por exemplo: se uma empresa deseja aumentar a produção e ao mesmo tempo reduzir os custos, pode descobrir que fazer uma ação para melhorar um desses objetivos pode prejudicar o outro.
Convex Hull
Em alguns contextos, problemas de otimização multiobjetivo podem envolver restrições geométricas. Além disso, em alguns problemas práticos, a representação gráfica do conjunto de soluções Pareto-ótimo (soluções que não podem ser melhoradas em um critério sem piorar em outro) pode ter uma forma convexa. O Convex Hull pode ser usado para modelar ou verificar restrições geométricas em um espaço de busca multiobjetivo, assim como para visualizar e entender melhor o conjunto de soluções Pareto-ótimo.
O Convex Hull (ou casco/feixe convexo) é uma envoltória convexa que engloba um conjunto de pontos no plano ou em um espaço multidimensional – ou seja, é a menor figura convexa que contém todos os pontos do conjunto. Existem vários algoritmos para calcular o Convex Hull, e alguns deles podem envolver uma aproximação do casco convexo. A aproximação pode ser usada para simplificar o cálculo do casco convexo em conjuntos de dados muito grandes ou complexos.
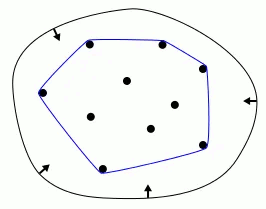
Para encontrar a casca convexa de um conjunto de pontos, pode-se usar um algoritmo chamado Graham Scan, que é considerado um dos primeiros algoritmos de geometria computacional. Usando este algoritmo, pode-se encontrar o subconjunto de pontos que estão no casco convexo, juntamente com a ordem em que esses pontos são encontrados ao contornar o casco convexo. Sucessivas iterações permitem obter o melhor conjunto de pontos.
O algoritmo de casco convexo pode ser aplicado como método de seleção de dados – trabalho importante na precisão das tarefas de classificação e regressão baseadas em modelos orientados a dados. No entanto, a utilização de implementações convencionais deste método em grandes dimensões, devido à sua alta complexidade, não é viável. Khosravani, Ruano e Ferreia (2016) propõem um algoritmo de casco convexo de aproximação que pode ser usado para dimensões altas em um tempo de execução aceitável e com baixos requisitos de memória, denominado approxHull, com melhor desempenho em comparação com a seleção aleatória de dados.
O conjunto de pontos do Convex Hull podem servir como entrada para um algoritmo genético, estando esses vértices compondo parte do conjunto de treinamento. Isso gera uma redução de dimensionalidade do espaço de busca, o que pode levar a uma busca mais eficiente, especialmente em problemas complexos com muitas variáveis de decisão. Além disso, o convex hull representa os limites externos do conjunto de pontos, o que pode ser útil se você estiver interessado principalmente nas soluções não dominadas (Pareto-optimal) que estão na fronteira externa do espaço de busca.
MOGA
As meta-heurísticas são estruturas algorítmicas genéricas, frequentemente inspiradas na natureza, projetadas para resolver problemas complexos de otimização e que costumam fazer poucas suposições sobre o problema a ser resolvido. Algoritmos evolutivos são uma classe de técnicas computacionais que se inspiram nos princípios da evolução biológica para resolver problemas de otimização, busca e aprendizado. Eles são baseados em modelos de evolução e seleção natural para encontrar soluções ótimas ou aproximadamente ótimas para problemas complexos.
Esses algoritmos são frequentemente utilizados em problemas de otimização nos quais se busca encontrar a melhor solução possível em um espaço de busca amplo e com múltiplas variáveis. Eles funcionam com uma população inicial de soluções e aplicam operadores genéticos, como seleção, recombinação (cruzamento) e mutação, para gerar novas soluções ao longo de várias gerações. Comparando os termos da genética com as definições matemáticas, temos que:
- O cromossomo é a representação das variáveis de decisão;
- O indivíduo é uma possível solução do problema, com valores calculados para função objetivo e restrições;
- A população é um conjunto de indivíduos (possíveis soluções) do problema, incluindo os indivíduos mais aptos (melhor valor na função objetivo) e os menos aptos (pior valor na função objetivo).
Os algoritmos evolutivos incluem várias técnicas, como Algoritmos Genéticos (GA), Programação Genética (GP), Estratégias Evolutivas (ES) e Programação Evolutiva (EP). Cada um desses métodos tem suas próprias características específicas de como manipulam as soluções candidatas e exploram o espaço de busca em direção a soluções melhores.
Uma solução A domina outra solução B se A for igual ou melhor que B em todos os objetivos e estritamente melhor em pelo menos um objetivo. Já uma solução é considerada não dominada se não for dominada por nenhuma outra solução no conjunto de soluções. A frente de Pareto consiste em todas as soluções não dominadas. Em problemas multiobjetivo, a busca ideal é encontrar um conjunto de soluções que cubra o maior espaço possível na frente de Pareto, representando compromissos entre os objetivos.
A classificação das soluções não dominadas (“non-dominated sorting”) é uma etapa crítica para atribuir a cada solução em uma população um número que indica sua posição na frente de Pareto. O objetivo é organizar as soluções em camadas (ou frentes), onde a primeira frente contém as soluções não dominadas, a segunda frente contém soluções dominadas apenas pela primeira frente, e assim por diante. Essa ordenação permite ao algoritmo focar em soluções de alta qualidade e diversidade na busca pelo conjunto de soluções de Pareto ótimo.
O MOGA (Multi-Objective Genetic Algorithm, ou Algoritmo Genético Multiobjetivo) é um tipo específico de algoritmo genético projetado para lidar com problemas de otimização multiobjetivo. Ele utiliza os princípios dos algoritmos genéticos (como seleção, cruzamento e mutação) para encontrar soluções que sejam ótimas em relação a múltiplos objetivos. Ou seja, realizar uma busca populacional do conjunto de Pareto de soluções de um determinado problema multiobjetivo.
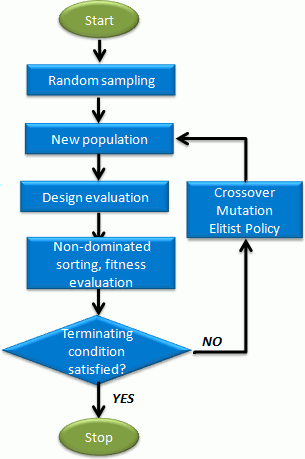
A execução começa com uma população inicial de indivíduos, a geração inicial, que é então avaliada e manipulada para calcular a população de indivíduos que compõem a próxima geração. Espera-se que, após um número suficiente de gerações, a população tenha evoluído, alcançando uma aproximação satisfatória à frente de Pareto. Sua operação basicamente segue o fluxo a seguir:
- Gerar população inicial
- Avaliar indivíduos no espaço objetivo
- Se o critério de parada for obtido, parar; caso contrário, prosseguir
- Atribuir aptidão a indivíduos
- Realizar seleção de acasalamento (“mating”)
- Recombinação (“recombination”)
- Mutação (“mutation”)
- Voltar ao passo 2
Neste caso, a cada indivíduo da população é atribuído um valor de aptidão e com base nesta aptidão os indivíduos são acasalados. Posteriormente cada par acasalado produzirá dois descendentes (“offspring”) pela aplicação do operador de recombinação, formando assim a próxima geração. Finalmente, o operador de mutação é aplicado a cada filho antes de repetir todo o processo.
De modo geral, se deseja maximizar a precisão (ou minimizar o erro) na previsão do valor do rótulo, enquanto minimiza a quantidade de “features” usadas, aqui está um guia simplificado de como usar MOGA para esse problema:
- Preparação dos Dados – Organizar um dataset onde cada rótulo possui um certo número de “features”, separando-os em conjuntos de treino, validação e teste.
- Definição do Modelo – Selecione um modelo de machine learning adequado para regressão, como regressão linear, árvores de decisão, random forest, redes neurais (como a do tipo RBF), etc.
- Avaliação do Modelo – Escolha uma métrica de avaliação para medir a precisão do modelo na previsão dos rótulos (Erro Quadrático Médio/MSE, Erro Médio Absoluto/MAE, etc) e combine a métrica de avaliação (que queremos maximizar ou minimizar) com a penalização pela quantidade de “features” usadas para criar uma função fitness. Por exemplo, você pode usar uma função que maximize a precisão e minimize a quantidade de “features” usadas, atribuindo pesos ou combinando essas métricas.
- Aplicação do MOGA – Segue conforme cronograma apresentado anteriormente, e considere definir critérios de parada, como número de gerações, convergência da solução, entre outros.
- Avaliação do Melhor Indivíduo – Após a execução do algoritmo, analise o melhor indivíduo encontrado para determinar as “features” mais importantes para a previsão dos rótulos.
- Teste do Modelo – Utilize o melhor conjunto de “features” encontrado para treinar o modelo final e avaliá-lo no conjunto de teste para avaliar seu desempenho.
Visando uma maior economia de recursos computacionais, você pode excluir features que não contribuam significativamente com o modelo e impor restrições de valores de erro e de complexidade. A verificação das features e dos valores é feita ao final de uma rodada do MOGA, sendo necessária uma nova rodada para implementar esses pontos.
Rede Neural RBF
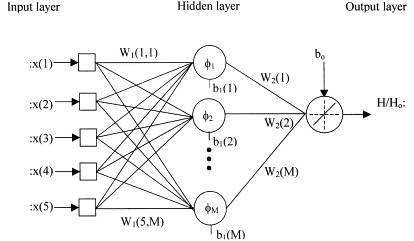
Dentre as opções de modelo acima citadas, está a Rede Neural de Função de Base Radial, ou RBF (Radial Basis Function) Neural Network em inglês. A RBF é um tipo específico de rede neural artificial caracterizado pelo uso de funções de base radial (valor depende da distância radial a partir de um ponto fixo) como funções de ativação em suas camadas ocultas. Sua estrutura básica consiste em três camadas:
- Camada de Entrada (Input Layer): recebe os dados de entrada (“features” e respectivos rótulos);
- Camada Oculta (Hidden Layer): composta por unidades de processamento que aplicam funções de base radial às entradas, onde cada unidade na camada oculta está associada a um centro e tem uma função de base radial que mede a proximidade entre a entrada e o centro;
- Camada de Saída (Output Layer): produz a saída da rede com base nas ativações da camada oculta.
O treinamento de uma RBF Neural Network envolve a determinação dos centros e larguras das funções de base radial na camada oculta, bem como os pesos associados na camada de saída. Isso geralmente é feito utilizando técnicas de otimização, como o algoritmo de retropropagação e algoritmos de otimização como gradiente descendente.
As RBF Neural Networks são aplicadas em uma variedade de áreas, incluindo reconhecimento de padrões, previsão de séries temporais e aproximação de funções matemáticas complexas. Elas têm a capacidade de representar relações não lineares de maneira eficiente, tornando-as úteis em problemas que não podem ser adequadamente abordados por métodos mais simples. Elas podem ser utilizadas para extrair características relevantes de imagens – por exemplo: as intensidades de pixel das imagens podem ser transformadas usando funções de base radial para mapeá-las para um espaço de características mais representativo.
Fontes
- Atsu S.S. Dorvlo, Joseph A. Jervase, Ali Al-Lawati, Solar radiation estimation using artificial neural networks, Applied Energy, Volume 71, Issue 4, 2002, Pages 307-319, ISSN 0306-2619, https://doi.org/10.1016/S0306-2619(02)00016-8.
- Ferreira, P. M., Martins, I. A. C., Ruano, A. E. (2010). Cloud and Clear Sky Pixel Classification in Ground-Based All-Sky Hemispherical Digital Images. IFAC Proceedings Volumes, Volume 43, Issue 1, Pages 273-278, https://doi.org/10.3182/20100329-3-PT-3006.00050.
- Martins, I. A. C. (2010). Neural models design for solar radiation and atmospheric temperature forecast. Dissertação. Universidade do Algarve. Faro, Portugal.
- Medium – Pascal Sommer – A gentle introduction to the convex hull problem