Suponha a seguinte situação: você criou um modelo de previsão de alguma variável e deseja saber seu desempenho, ou seja, em quais dias/meses/anos ele faz melhores previsões e a partir de quantos períodos as previsões deixam de ser confiáveis. Segue uma sugestão de como organizar os dados e as métricas utilizadas para fazer essas comparações – os códigos estão disponíveis no GitHub/accuracy.
Uma forma de organizar os dados para sua visualização mais compacta é através de uma tabela onde as linhas são as rodadas (identificadas pela data da primeira previsão realizadas) e as colunas são as previsões em si (indicadas pelo número da coluna, que indica o avanço de tempo de cada uma):
| n1 | n2 | … | nN | |
|---|---|---|---|---|
| run1 | ||||
| run2 | ||||
| … | ||||
| runM |
Por exemplo, para 10 rodadas (runs) com previsões mensais para os próximos 12 meses (N = 12 e M = 10), a coluna “n1” possui os primeiros valores previstos para cada rodada, e assim por diante. Para saber a data da respectiva previsão, basta somar o número da coluna menos 1 à data que identifica a rodada. Por exemplo, chamando a coluna 0 como a que contém as datas iniciais das previsões, para obter a data de previsão cuja rodada inicia em 2014-01, para essa linha, a 1ª coluna tem data 2014-01, a 2ª coluna tem data 2014-05 e assim por diante. Nas linhas seguintes, repete-se o raciocínio.
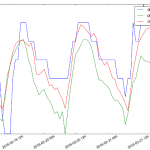
Assim, agrupando-se os valores pelas colunas, têm-se o comportamento por ordem de previsão na rodada (por exemplo, 1° mês previsto, 2° mês previsto, …). Ao seguir uma diagonal ascendente, é possível comparar a previsão para uma mesma data, mas de rodadas diferentes.
Como exemplo, você pode usar os dados seguintes públicos
- índices climáticos calculados pela Administração Oceânica e Atmosférica Nacional dos EUA (NOAA): ftp://ftp.cpc.ncep.noaa.gov/wd52dg/data/indices/sstoi.indices
- previsões de índices climáticos do Serviço Meteorológico do Canadá (WeatherCAN): http://dd.weather.gc.ca/ensemble/cansips/csv/indices/hindcast/monthly/
Boa parte das previsões (rodadas anteriores a 2017-07) são de hindcast: também conhecido como re-forecast histórico, integra o modelo para frente no tempo, assim como com uma previsão, mas iniciando em algum instante no passado. O objetivo de um hindcast é fazer a previsão novamente usando algo que não estava disponível originalmente.
De todas as variáveis disponíveis, o script está configurado para pegar as anomalias de temperatura da superfície do mar (SST, do inglês “sea surface temperature”) na região “Niño 3.4” do Oceano Pacífico – veja mais no site da WeatherCAN.
Métricas usadas
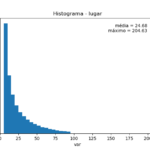
O erro é a diferença entre um valor medido (ou calculado/previsto) e um valor verdadeiro (ou observado) de uma grandeza. Uma métrica muito usada para avaliar o erro de um modelo é a média percentual absoluta do erro (MAPE, do inglês “Mean Absolute Percentage Erro”):
\(MAPE=\frac{1}{n}\sum\limits_{t=0}^{n-1}|(y_t-y’_t)/y_t|\times100%\)
Onde \(y_t\) é o valor observado e \(y’t\) é o calculado. Os erros percentuais têm a vantagem de serem independentes da escala, no entanto têm a desvantagem de serem infinitas ou indefinidas se o valor observado é igual a zero (ou tende a valores extremos quando qualquer o valor observado é próximo de zero). Outras observações podem ser vistas nessa resposta do stackexchange.
O conceito de acurácia costuma ser aplicado para amostras discretas. Ou seja, são usadas tabelas de contingência para contabilizar se o valor previsto foi:
- previsto e observado (verdadeiro positivo)
- previsto mas não obtido (falso positivo)
- não previsto mas observado (falso negativo)
- não previsto nem observado (verdadeiro negativo)
Assim, a acurácia é definida como a razão dos acertos sobre os erros, seguindo essa tabela. Para uso comercial, o MAPE é frequentemente preferido porque aparentemente os gerentes entendem percentuais melhor que os erros quadrados.
Para variáveis contínuas, é necessário considerar a incerteza da precisão (e não o valor exato) para classificar nos casos do quadro. No entanto, também existem outras definições (fontes: stackexchange e better buiness analytics):
\(Acurácia = 100 – MAPE\)
Desse modo, quando o erro for zero (0%), a acurácia é de 100% (acerto total); se o erro for 100%, a acurácia é de 0%. Caso o erro seja maior do que 100%, isso implica em acurácia negativa, mostrando que a previsão está realmente muito ruim.
Pensando em ordem de previsões por rodada, é impressa na tela a mediana das acurácias de cada coluna (pois evita alguns extremos de rodadas muito ruins).
Cálculos usando os scripts python
Baixe os arquivos no GitHub/accuracy e crie a pasta “data”. Baixe os arquivos para as subpastas “forecast” (previsões) e “observation” (observados), dentro da pasta “data”. O script principal é o “accuracy.py” e as funções estão no arquivo “functions.py”, na pasta “helpers”.
No script principal, defina os nomes das variáveis analisadas (tem um nome no arquivo dos dados observados e outro dos previstos), além da ata de início da primeira previsão (no formato YYYMM), conforme os exemplos que já constam dos scripts.
Nos scripts, a parcela de cada valor de MAPE e de acurácia são calculados individualmente, para serem impressos em uma tabela como arquivo CSV (na pasta “data”). A interpretação dessa tabela está no começo do post.
Na tela, é impressa a acurácia para cada ordem de rodada. Quanto mais arquivos de previsão forem utilizados, mais será visível o comportamento de queda da acurácia quanto maior for o número da previsão – segue quase uma curva exponencial.