Modelo ARIMA e previsão no R

O software livre R contém pacotes muito utilizados para trabalhar com estatística – em particular para elaborar modelos ARIMA. As rotinas devem envolver, basicamente:

Ler arquivos CSV com as variáveis observadas e a previsão de regressores (se for o caso) em função do tempo
Análise de auto correlação
Construir modelo ARIMA
Previsão usando o modelo
Gráfico dos resultados (acertar limites e linhas exibidas)

Além do próprio programa R, também deve ser instalado o pacote “forecast” – veja mais sobre linguagem R clicando no link. Esse pacote possui funções de previsão para séries de tempo e modelos lineares, como:

BoxCox() – retorna o reultado de uma transformação “Box-Cox”: f(x)=(x^lambda-1)/lambda
BoxCox.lambda() – calcula o parâmetro lambda da transformação Box-Cox
Arima() – ajusta o modelo ARIMA à série de dados univariada (função com uma só variável)
auto.arima() – retorna o melhor ajuste ao modelo ARIMA
forecast() – função genérica para uma série temporal ou modelo de série temporal.

A função ts() (do inglês time serie) considera a série temporal com os dados igualmente espaçados, a variável tempo não precisa ser dada explicitamente. Desse modo, é necessário somente informal o início da série e sua frequência (“freq/frequency”). O formato é ts(vector, start=, end=, frequency=); veja alguns exemplos:

# Dados anuais - não se utiliza o parâmetro 'frequency'
ts(dados, start = 2001)
# Dados mensais - informar ano e mês
ts(dados, start = c(2001,06), frequency = 12)
#Dados trimestrais - informar ano e trimestre
ts(dados, start = c(2001,1), frequency = 4)
#Dados diários - informar ano e dia do ano
ts(dados, start = c(2001,152), frequency = 365)

A função auto.arima() do R usa uma variação do algoritmo desenvolvido por Hyndman e Khandakar que combina testes de raiz unitária, minimização de AICc e MFV para obter um modelo ARIMA. As etapas do algoritmo podem ser vistas no link. A função auto.arima retorna uma lista com: coef, sigma2, var.coef, mask, loglik, aic, arma, residuals, call, series, code, n.code, model (phi, theta, delta, Z, a, P, T, V, h, Pn), bic, aicc, xreg, x e lambda, respectivamente.

Dentre os parâmetros (opcionais) da função auto.arima, estão:

stationary: TRUE para restringir a pesquisa para modelos estacionários.
xreg: vetor/matriz de regressores (“regressors”) externa. São pesos dados às observações da série temporal.
stepwise: TRUE fazer a seleção stepwise (default). Caso contrário, ele procura sobre todos os modelos – pode ser muito lenta, especialmente para os modelos sazonais.
trace: TRUE para imprimir os modelos considerados
approx/approximation: TRUE para estimativa através de somas condicionais quadráticas e os critérios de informação utilizados para seleção de modelos são aproximadas. O modelo final ainda é calculado usando estimativa máxima verossimilhança. A aproximação deve ser usado para a série de longa data ou um período muito sazonal para evitar tempos excessivos de computação.
seasonal: Se FALSE, restringe a pesquisa para modelos não- sazonais.
ic: informa o critério de seleção a ser utilizado (por default, ic=”aicc”)

A função auto.arima retorna o modelo escolhido (conforme os valores de p, d e q), os termos autorregressivos (arX) e de média móvel (maX), de “drift” (termo constante em modelo que tem d > 0 devido à sazonalidade), “intercept” (média do termo (1-L)^dXt, próximo à média da série histórica) e dos regressores (se for o caso), assim como o erro/desvio padrão (s.e. – “standard error”) de cada valor apresentado. Como o desvio padrão mostra o quanto de variação ou “dispersão” existe em relação à média (ou valor esperado), se todos os pontos estiverem exatamente sobre a linha de regressão, então regressão explicaria toda a variação, ou seja, s.e. seria igual a zero. A função também imprime os critérios de informação AIC, AICc e BIC, assim como o log do MFV (log likelihood) e a variância (sigma^2), que é definida como o quadrado do desvio padrão. Veja um exemplo (diferente dos dados usados nos gráficos):

Series: exemplo
Series: resid 
ARIMA(1,1,1)(1,0,1)[12]

Coefficients:
         ar1      ma1    sar1     sma1    prec
      0.5488  -0.9031  0.8937  -0.7234  0.0029
s.e.  0.1212   0.0694  0.1037   0.1601  0.0006

sigma^2 estimated as 0.1234:  log likelihood=-45.31
AIC=102.62   AICc=103.37   BIC=119.3

Nesse exemplo, houve uma derivação, um de autorregressão e um de médias móveis. O segundo conjunto de parênteses refere-se ao modelo desenvolvido para a parte sazonal, cujos coeficientes recebem um “s” na frente. O valor dentro dos colchetes é o número de períodos por temporada. Se a soma dos coeficientes de AR é próxima de 1, isso que mostra que os parâmetros estão perto da borda da região de estacionaridade.

O número de linhas dos regressores deve ser o mesmo da série temporal. O modelo criado por arima() e auto.arima() com um argumento xreg é uma regressão linear com erros ARMA:

\(y_t=\beta x_t+\eta_t\)
\(\eta_t=\phi_1\eta_{t-1}+…+\phi_p\eta_{t-p}-\theta_1Z_{t-1}-…-\theta_qZ_{t-q}+Z_t\)

Onde:

yt é o valor da projeção no instante t
xt é a covariância no instante t e β é seu coeficiente;
Φ é o polinômio ligado ao operador autorregressivo de ordem p;
θ é o polinômio ligado ao operador de média móveis de ordem q;
zt é o ruído branco no instante t.

Mais informações nesse link.

Outro pacote em R bom para esse tipo de estatística é o ASTSA. Nele, é possível plotar gráficos de ACF, PACF, p-value, possui filtros, técnicas e várias séries de dados para serem usadas como exemplo.

Previsão

Do mesmo pacote do R, existe a função “forecast”, que chama a função “predict”. Quando é feita a previsão com um modelo ARIMA sem regressores, ele simplesmente usa os valores passados de sua série histórica para prever valores futuros. Nesse caso, você pode especificar o seu horizonte “h”, que limita os períodos de previsão.

Ao usar regressores para construir um modelo ARIMA, é preciso incluir valores futuros dos regressores – o parâmetro “h” é ignorado. Por exemplo, se você usou temperatura como regressor para prever a incidência de uma doença, então você precisaria de valores futuros de temperatura para prever a incidência da doença.

A função forecast retorna uma lista composta de: method, model, level, mean, lower, upper, x, xname, fitted e residuals, respectivamente.

A variável de entrada level é opcional e representa os níveis/intervalo de confiança – intervalo estimado onde a média tem uma dada probabilidade de ocorrer, que no caso do exemplo abaixo são as opções 65% (cinza claro) e 80% (cinza escuro). Sua interpretação seria algo como “existe 80% de probabilidade de que o cálculo do intervalo de confiança de alguns experimentos futuros envolvam o valor verdadeiro do parâmetro da população”. Veja mais no blog do Rob Hyndman.

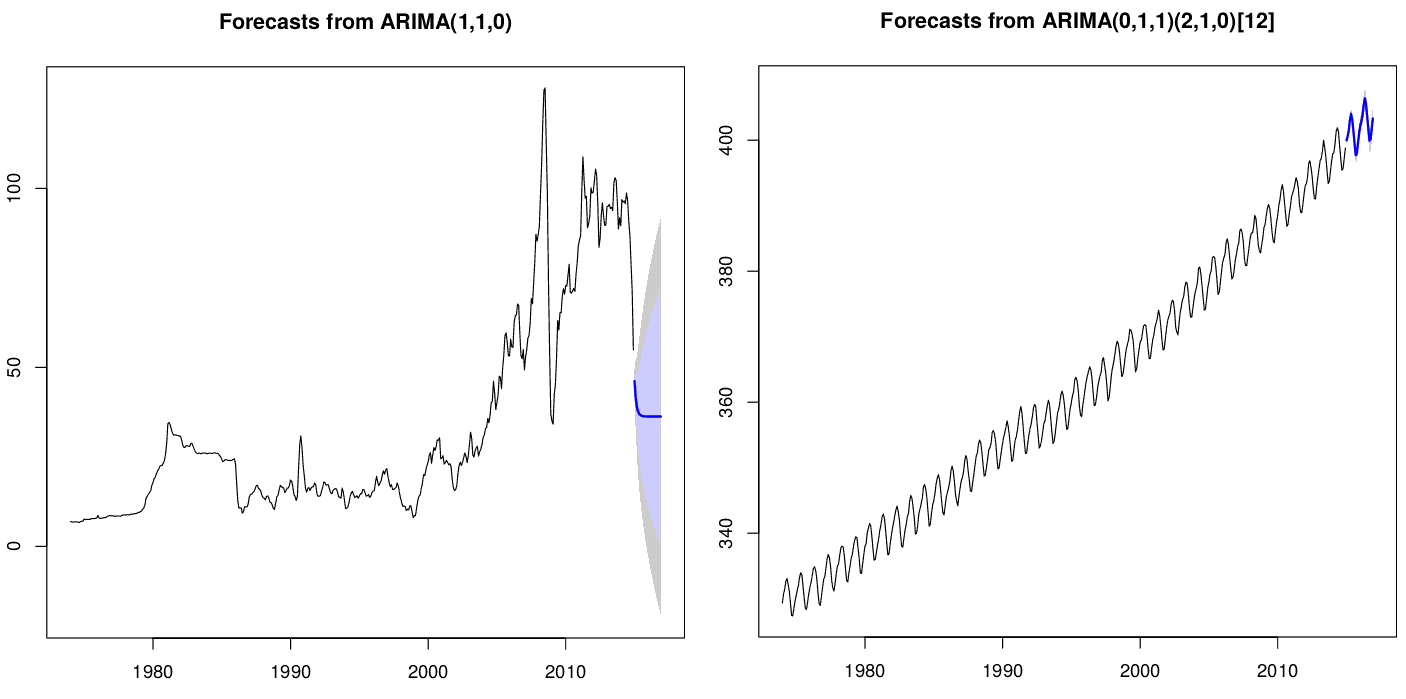
Gráfico com dados observados, modelo e projeção das séries de preço de barril de petróleo (esq.) e concentração de CO2

O gráfico da série temporal de valores observados junto com os valores modelados para esse período e a previsão com os respectivos intervalos de confiança pode ser plotado através do R com as seguintes linhas:

# Ler dados observados de arquivo CSV
dados.obs = read.csv(filepath, header = TRUE)
# Criar série temporal com uma coluna dos dados observados
dados.ts = ts(dados.obs$valor, frequency = 12, start = c(start.year.hist, start.month.hist))
# Fazer modelo ARIMA
model = auto.arima(dados.ts)
# Projeção 
forec = forecast(model, level = c(65,80))
# Impressão de gráfico com série temporal e projeção com intervalos de confiança
plot(forec)
# Incluir no gráfico os valores do modelo para dados observados em azul
lines(fitted(model),col="blue")

O código para fazer o gráfico em si corresponde às duas últimas linhas não comentadas, sendo que as linhas anteriores correspondem a leitura de dados, modelagem e previsão. Note que “forec” é a saída da função “forecast”.

Fontes